This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs License which permits noncommercial use and distribution provided the original author(s) and source are credited. (See https://creativecommons.org/licenses/by-nc-nd/4.0/
NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Structured Abstract
Background:
Patient-centered outcomes research (PCOR) can be successful only with valid analytics. The routine operation of the US health care system produces an abundance of electronically stored data that capture the care of patients as it is provided in settings outside of controlled research environments. The potential for using these data to inform future treatment choices and improve patient care and outcomes in the very system that generates the data is widely acknowledged. Given these key properties of secondary data and the abundance of electronic health care databases covering millions of patients, it is critical to strengthen the rigor of causal inferences that can be drawn from such data. Innovative analytic approaches based on defined algorithms that will maximize confounding control have recently been developed—high-dimensional propensity score (HDPS) and collaborative targeted maximum likelihood estimation (CTMLE)—that (1) are grounded in epidemiological principles of causal inference and (2) maximize confounding adjustment in a given data source. Their performance is not well understood in many relevant settings. We will evaluate such methods in empirical studies and complex simulations based on empirical data structures.
Objectives:
Implement, adapt, and compare novel algorithmic approaches for improved confounding control in comparative effectiveness research (CER) using available health care databases. Using simulation studies, we will characterize and optimize the performance of these algorithms, then disseminate insights concerning these methods through publications and symposia/conferences and provide an interactive webpage with free software and result libraries.
Methods:
We evaluated the performance of data-adaptive algorithms for variable selection and propensity score (PS) estimation using both simulations and empirical examples that reflect a range of settings common to large electronic health care databases. The algorithms included the HDPS, a combination of super learner (SL) prediction modeling and HDPS, a modified version of CTMLE that is scalable to large health care databases, and many traditional machine learning algorithms. We based simulations on the plasmode framework in which empirical data are incorporated into the simulation process to more accurately reflect the complex relations that occur among baseline covariates in practice.
Results:
Overall, the basic heuristic of variable reduction in the HDPS adjustment performed well in diverse settings. However, the HDPS can be sensitive to the number of variables included for adjustment and severe overfitting of the PS model can negatively impact the properties of effect estimates. Combining the HDPS with the modified version of CTMLE performed well for many of the scenarios considered but was sensitive to parameter specifications within the modified algorithm. Combining the HDPS with SL was the most consistent selection strategy and may be promising for semiautomated data-adaptive PS estimation and confounding control in high-dimensional covariate data sets.
Conclusions:
This project provides guidance on the optimal use and advantages of novel data-adaptive methods for variable selection and PS estimation for CER. This project is the first to adapt, test, and improve novel approaches based on the combination of SL, CTMLE, and HDPS for variable selection and confounding control in CER using routine care data. We found that combining the HDPS with SL prediction modeling is promising for data-adaptive PS estimation in large health care databases. We provided free software with instructions and guidance to enhance the utility of the proposed methods.
Limitations and Subpopulation Considerations:
The application of data-adaptive algorithms in electronic health care data is promising, but no single method was optimal across all data sets and scenarios. While plasmode simulations and empirical examples allow investigators to evaluate methods in settings that reflect real-world practice, they also make it difficult to elucidate reasons for observed differences in the performance across methods. This project provides strong evidence for the utility of data-adaptive algorithms in electronic health care data—in particular the combination of SL with the HDPS—and provides guidance and software for implementing the recommended tools. However, more research is needed to elucidate specific factors that influence the performance of the discussed methods.
Background
Patient-centered outcomes research (PCOR) can be successful only with valid analytics. The routine operation of the US health care system produces an abundance of electronically stored data that capture the care of patients as it is provided in settings outside of controlled research environments. The potential for using these data to inform future treatment choices and improve patient care and outcomes in the very system that generates the data is widely acknowledged,1 although these data are still underused for evidence generation.2 Particularly for elderly multimorbid patients and other vulnerable patient groups who are often excluded from randomized trials, these data, properly analyzed, are key to improving care. Further, such secondary data reflect the health outcomes as they occur in routine care, a main goal of PCOR.
Despite the long list of potential advantages of evaluating drug effects in existing databases—speed, statistical power, reflecting routine health care, and inclusion of elderly patients and those with multiple medical conditions—the greatest challenge remains bias caused by confounding by indication due to selective prescribing based on disease severity and patient prognosis.3,4 With limited confounder information and in the absence of a randomized treatment assignment, it may be difficult to distinguish between an outcome resulting from a drug treatment and one due to the underlying disease for which the drug was prescribed. Several prominent studies have failed due to this challenge, including nonrandomized studies on the effectiveness of statin medications.5-10
A fundamental flaw of current approaches to mitigate confounding in health care database analyses is that they rely on the investigator to specify all factors that may confound a causal drug–outcome association. Most investigators fail to identify all confounders because, in fact, some empirical confounders are unknown at the time of ground-breaking research. Further, traditional outcome regression modeling, propensity score (PS) methods, and data mining approaches generally rely on a limited number of investigator-defined covariates (often <50).11
Health care databases (claims, electronic health records, most registries) are as much a description of medical sociology under economic constraints as they are records of delivered health care.12 Consequently, information contained in such databases may be understood and analyzed as a high-dimensional set of proxy factors that indirectly describe the health status of patients through several lenses, most importantly the lenses of health care access and the treating physician.2 Once candidate proxies or patterns that stand in for the underlying conditions are identified, methods for assessing their relevance to the study at hand are well established.13,14 Analytic methods are likely to receive more accurate and precise results with algorithmic approaches that use empirical associations in the data to identify variables that are strongly associated with both treatment and outcome (empirical confounders), which can then be used to supplement investigator-identified confounders to improve confounding control in high-dimensional covariate spaces through proxy adjustment.15-17 Such proxy-based approaches are just beginning to penetrate comparative effectiveness research (CER) but show high promise.18
The high-dimensional propensity score (HDPS) is becoming one of the more widely used semiautomated variable selection algorithms for proxy-based adjustment in comparative effectiveness studies using electronic health care databases.19 A growing body of evidence shows that the HDPS can often improve confounding control when used to complement expert knowledge for variable selection.20-22 Although the algorithm can complement expert knowledge to improve confounding control, the challenge of determining which and how many of the HDPS-generated empirical confounders to include in the adjustment set remains.
When working with secondary data that were not collected for research purposes, it is recommended that investigators be generous when specifying the number of variables for adjustment, since empirically identified confounders can sometimes act as proxies for unmeasured factors.19 While this approach increases the likelihood of adjusting for instrumental variables or colliders, simulation studies have shown that the increase in bias— which can occur when adjusting for such variables—is generally small compared with the bias caused by excluding confounding variables.23,24 Rassen et al16 further argued that overfitting is not the primary concern when modeling the PS since the goal of the PS is to remove imbalances in the data at hand rather than to be generalizable to other data sets. In electronic health care data, however, potentially thousands of variables are available to be selected as empirical confounders. In these settings selection rules that are too generous can be impractical and lead to overparameterized and unstable PS models. The effects of overfitting these models are not well understood, and how analysts can determine the optimal number of empirical confounders for adjustment in high-dimensional covariate settings remains unclear.
In this study, we compared several data-adaptive algorithms for prediction modeling and variable selection when estimating PSs within electronic health care data sets. We considered a library of algorithms that consists of both nonparametric and parametric models. We also considered novel strategies for prediction modeling that combine the HDPS with SL prediction modeling, collaborative targeted maximum likelihood estimation (CTMLE), and other penalized regression.25-29 We then evaluated the performance of these methods using real empirical examples and plasmode simulations, which incorporate empirical data into the simulation structure to preserve the complex relations among baseline covariates that are observed in real-world practice.30
The overarching aims of our research were to develop, implement, adapt, and compare novel data-adaptive algorithmic approaches for variable selection and prediction modeling that can be used in combination with the HDPS to help researchers improve confounding control in large health care databases. These novel methodological tools have the potential to improve the rigor of causal inference in CER when using secondary health care databases to evaluate associations between medical products and clinical outcomes. Using both real-world data and simulation studies, we aim to characterize and optimize the performance of these algorithms and disseminate insights concerning these methods through publications and symposia/conferences, and to provide an interactive webpage with free software and result libraries.
Participation of Patients and Other Stakeholders in the Design and Conduct of Research and Dissemination of Findings
The Division of Pharmacoepidemiology (DoPE) Patient Advisory Board is an organization of patients who demonstrate above-average knowledge of navigating health care systems as well as an interest in treatment safety and efficacy. The board was established to guide DoPE's research toward patient-centered outcomes. Meeting each quarter, members assist investigators by (1) identifying key problems they encounter in health care delivery; (2) advising on the most important questions of interest in comparative effectiveness research; (3) acting as a sounding board for consumer-facing study materials; (4) representing patients' voices in all stages of research conduct; and (5) helping ensure that key findings are disseminated in ways that are accessible to patients and families. Dr Schneeweiss met with the DoPE Stakeholder Engagement Group. He began by orienting the group with background material on the benefits and challenges of conducting patient-centered comparative effectiveness research in administrative databases; he then provided an overview of the project and the plans for the coming months. He received many questions and comments from the group. Dr Schneeweiss also met with this group to provide updates on the progress of the project and to receive ongoing input.
Methods
The methods section is broadly divided into 2 parts: Section 1 will describe the methods used in the evaluation of numerous prediction algorithms in estimating the PS using 3 empirical data sources. Section 2 will describe the methods used in the plasmode simulations.30 Plasmode simulations allow us to construct simulated data for which true causal associations are known while maintaining the complex relations between baseline covariates that are observed in practice. The basic principle of plasmode data sets is to take the observed data structure, change the outcome status according to an imposed relationship between the outcome with both treatment and baseline covariates, and analyze the resulting data using the methods for comparison. This approach is increasingly used for methodological research in both genomics and pharmacoepidemiology.30 The resulting simulated data sets have a known exposure effect, but the correlation structure between baseline covariates and treatment assignments remains unaltered. Since all associations between baseline covariates with the outcome are simulated, all confounding variables along with the true treatment effect are known by design. Therefore, we can compare the performance of various methods for confounding control within simulated data that maintains much of the data complexity observed in practice. We will work with several data sources, which will provide variation in the underlying empirical data structure. We followed an analysis plan that outlined how the simulation setup would be constructed.
Evaluating Prediction Algorithms Using Empirical Data
Data Sources and Study Cohorts
We used 3 data sets in the evaluation of the predictive performance of various data-adaptive algorithms (Table 1): the Novel Oral Anticoagulant Prescribing (NOAC) data set, the Nonsteroidal Anti-inflammatory Drugs (NSAID) data set, and the Vytorin data set. These data sets have been described in previous studies, and descriptions are provided in the Appendix.16,19,31 Each data set consisted of 2 types of covariates: baseline covariates that were selected a priori using expert knowledge, and claims codes. Baseline covariates include demographic variables (eg, age, sex, census region, race) and other predefined covariates that were selected a priori using expert knowledge. Claims codes included information on diagnostic, drug, and procedural insurance claims for individuals within the health care databases.
Table 1
Summary of Methods Evaluated in Data Applications and Plasmode Simulations.
- NOAC study. The NOAC data set was generated to track a cohort of new users of oral anticoagulants to study the comparative safety and effectiveness of warfarin vs dabigatran in preventing stroke. United Healthcare collected the data between October 2009 and December 2012. The data set includes 18 447 observations, 60 baseline covariates, and 23 531 claims code covariates. Each claims code within the data set records the number of times that the specific code occurred for each patient within a prespecified baseline period before initiating treatment. The claims code covariates fall into 4 categories, or data dimensions: inpatient diagnoses, outpatient diagnoses, inpatient procedures, and outpatient procedures.
- NSAID study. The NSAID data set was constructed to compare new users of a selective COX-2 inhibitor with those using a nonselective NSAID in the risk of gastrointestinal bleed. The observations were drawn from a population of patients aged 65 years and older enrolled in both Medicare and the Pennsylvania Pharmaceutical Assistance Contract for the Elderly programs between 1995 and 2002. The data set consists of 49 653 observations, with 22 baseline covariates and 9470 claims code. The claims code covariates fell into 8 data dimensions: prescription drugs, ambulatory diagnoses, hospital diagnoses, nursing home diagnoses, ambulatory procedures, hospital procedures, doctor diagnoses, and doctor procedures.
- Vytorin study. This data set was generated to track a cohort of new users of Vytorin and high-intensity statin therapies. The data were collected to study the effects of these medications on the combined outcome, myocardial infarction, stroke, and death. The data set includes all United Healthcare patients who were aged 65 years or older on the day of entry into the study cohort and covers the period of January 1, 2003, to December 31, 2012. The data set includes 148 327 observations, 67 baseline covariates, and 15 010 code covariates. The claims code covariates fell into 5 data dimensions: ambulatory diagnoses, ambulatory procedures, prescription drugs, hospital diagnoses, and hospital procedures.
For each data set, we randomly selected 80% of the data as the training set and the rest as the testing set. We centered and scaled each of the covariates as some algorithms are sensitive to the magnitude of the covariates. We conducted model fitting and selection on only the training set and assessed the goodness of fit of all the models on only the testing set to ensure objective measures of prediction reliability.
The HDPS
The HDPS is an automated variable selection algorithm designed to identify confounding variables within electronic health care databases. Health care claims databases contain multiple data dimensions, where each dimension represents a different aspect of health care use (eg, outpatient procedures, inpatient procedures, medication claims). When implementing the HDPS, the investigator first specifies how many variables to consider within each data dimension. Following the notation of Schneeweiss et al,19 we let n represent this number. For example, if n = 200 and there are 3 data dimensions, then the HDPS will consider 600 codes. For each of these 600 codes, the HDPS then creates 3 binary variables labeled frequent, sporadic, and once, based on the frequency of occurrence for each code during a covariate assessment period before the initiation of exposure. In this example, there are now a total of 1800 binary variables. The HDPS then ranks each variable based on its potential for bias using the Bross formula.13 Based on this ordering, investigators then specify the number of variables to include in the HDPS model, which is represented by k.
Machine Learning Algorithm Library
We evaluated the predictive performance of a variety of machine learning algorithms available within the caret package (version 6.0)40 in the R programming environment. These algorithms are summarized in Table 1. Due to computational constraints, we screened the available algorithms to include only those that were computationally less intensive. Because of the large size of the data, we used leave group out (LGO) cross-validation instead of V-fold cross-validation to select the tuning parameters for each individual algorithm. We randomly selected 90% of the training data for model training and 10% of the training data for model tuning and selection. For clarity, we refer to these subsets of the training data as the LGO training set and the LGO validation set, respectively. After the tuning parameters are selected, we fit the selected models on the entire training set and assess the models on the testing set. The split could be different for different algorithms.
Super Learner
The SL is a method for selecting an optimal prediction algorithm from a set of user-specified prediction models. The SL relies on the choice of a loss function (negative log likelihood in the present study) and the choice of a library of candidate algorithms.25,27 The SL then compares the performance of the candidate algorithms using V-fold cross-validation; for each candidate algorithm, SL averages the estimated risks across the validation sets, resulting in the so-called cross-validated risk. Cross-validated risk estimates are then used to compute the best weighted linear convex combination of the candidate learners with the smallest estimated risk. This weighted combination is then applied to the full study data to produce a new set of predicted values and is referred to as the SL estimator. The SL has been shown to perform asymptotically as well as or better than the best-performing user-specified model in terms of minimizing the cross-validated loss function for a specified measure of predictive performance.25 The advantage of the SL is that it is able to consider many prediction models and take advantage of the individual strengths of the best-performing models for the given data set.
Due to the computational constraints, in this study we used LGO validation instead of V-fold cross-validation. We first fit every candidate algorithm on the LGO training set then computed the SL weight on the LGO validation set. This is a so-called sample split SL algorithm. We used the SL package in R (version 2.0-15.0) to evaluate the predictive performance of 2 SL estimators:
- SL1 included only baseline variables with all 23 of the previously identified traditional machine learning algorithms (Table 1) in the SL library.
- SL2 is identical to SL1, but with the addition of the HDPS algorithms with different tuning parameters in its SL library. Note that only the HDPS algorithms had access to the claims code variables in SL2.
Performance Metrics
We used 3 criteria to evaluate the prediction algorithms: computing time, negative log likelihood, and area under the curve (AUC). In statistics, a receiver operating characteristic (ROC), or ROC curve, is a plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. The curve is created by plotting the true positive rate against the false-positive rate at various threshold settings. The AUC is then computed as the area under the ROC curve. For both computation time and negative log likelihood, smaller values indicate better performance, whereas for AUC the better classifier achieves greater values.32 Compared with the error rate, the AUC is a better assessment of performance for the unbalanced classification problem.
Evaluating Methods Using Plasmode Simulations
The HDPS and Challenges in Determining the Number of Variables for Adjustment
The optimal number of variables to include in an HDPS model varies according to the properties and structure of a given data set. Model selection for the HDPS is further complicated since there is no clear approach for how to best compare the relative performance of PS models that control for different sets of variables. Traditional approaches for PS model selection and validation have primarily included metrics that assess covariate balance across treatment groups after PS adjustment.33-36 While balance metrics may be the most direct approach for comparing PS models that include a common set of variables, it is unclear how balance metrics can inform the selection process when comparing PS models that include different covariate sets, since these models will naturally enforce balance on different sets of variables. Here, we investigate whether alternative data-adaptive approaches based on cross-validated prediction diagnostics, collaborative targeted learning, and penalized regression can be combined with the HDPS algorithm to potentially improve the robustness of PS estimation in high-dimensional covariate settings.
Combining SL Prediction Modeling With the HDPS
In theory, analysts can combine SL with the HDPS to simplify PS estimation in high-dimensional covariate settings. When the optimum number of variables for adjustment is not known, analysts can run many HDPS models with various numbers of variables included in them. The SL can then be run on all these regressions to get the SL predictions. These predictions will be similar to those from the regression with the optimum number of important variables, in terms of minimizing a cross-validated loss function for predicting treatment assignment. A detailed description of SL is provided by van der Laan et al,25 while Rose37 and Pirracchio et al38 provide descriptions targeted to epidemiologic audiences.
Selection rules for PS models based on minimizing prediction error for treatment may seem contradictory to previous studies that have discussed how the goal of the PS is not to predict treatment assignment but to control confounding by balancing risk factors for the outcome across treatment groups.39-41 A primary reason for this lack of correspondence between treatment prediction and confounding control is the inclusion of instrumental variables (ie, variables that affect treatment but are unrelated to the outcome except through treatment). Including instruments in PS models improves treatment prediction but also negatively impacts the properties of effect estimates.23,42,43 By first using the HDPS algorithm to identify and rank variables based on their potential for bias, however, a variable's relationship with the outcome is taken into account in the selection process. Using the HDPS to screen strong instruments before implementing SL prediction modeling can not only potentially improve the correspondence between treatment prediction and confounding control but also simplify PS estimation in high-dimensional covariate data sets.
Scalable CTMLE
CTMLE is an extension of the doubly robust targeted maximum likelihood estimation (TMLE) method.28 TMLE consists of fitting an initial outcome model to predict the counterfactual outcomes for each individual and then using the estimated PS to fluctuate this initial estimate to form a new set of predicted values that optimize a bias/variance tradeoff for a specified causal parameter (ie, the treatment effect). For a detailed discussion on TMLE and CTMLE, see Gruber and van der Laan.26,28 Discussions on TMLE targeted toward general epidemiologic audiences are provided by Pang et al44 and Schuler and Rose.45 A discussion on the basic logic and objectives of the CTMLE algorithm is provided in the Appendix.
CTMLE extends TMLE by using an iterative forward selection process to construct a series of TMLE estimators, where each successive TMLE estimator controls for 1 additional variable and then selects the estimator that minimizes the cross-validated prediction error for the outcome. Unlike the HDPS algorithm, which assesses a variable's potential for confounding through marginal associations with both treatment and outcome, CTMLE considers how a variable both relates to treatment assignment and contributes to the cross-validated prediction for the outcome after conditioning on a set of previously selected variables. Variable selection methods that take into account a variable's conditional association with both treatment and outcome can, in theory, improve the properties of effect estimates by reducing the likelihood of controlling for variables that are conditionally independent of the outcome after adjusting for a set of previously identified confounders. To make CTMLE computationally scalable to large data, the CTMLE algorithm can be modified to include preordering of variables to avoid the iterative process of searching through each variable in the selection procedure. An overview of the scalable collaborative targeted MLE algorithm is provided in the Appendix. A detailed discussion on scalable CTMLE is provided by Ju et al.46
Regularized Regression With HDPS variables
Regularized regression models use penalized maximum likelihood estimation to shrink imprecise model coefficients toward 0. Recent studies have shown that regularized regression models can perform well for variable selection in high-dimensional covariate data sets.20,47 Franklin et al20 found that least absolute shrinkage and selection operator (LASSO) regression may be particularly useful for variable selection, especially when used in combination with the HDPS algorithm. Franklin et al20 showed that LASSO regression can be used to identify a subset of HDPS variables for adjustment by fitting a LASSO model to the outcome as a function of a large set of such variables, then selecting the variables with coefficients that are not shrunk to 0 within the LASSO model. This set of variables then forms the adjustment set and can be used to estimate the PS.
Plasmode Simulations
We evaluated the performance of the described methods using a plasmode simulation framework in which empirical data are incorporated into the simulation process in order to more accurately reflect the complex relations that occur among baseline covariates in practice.30 We constructed simulations based on the 3 empirical data sets (NSAID, NOAC, and Vytorin) previously described. For each individual within each data set, we identified all diagnostic codes, procedural codes, and medication claims occurring within a prespecified washout period before his or her treatment index date. We selected the 200 most prevalent codes and used logistic regression to model the observed outcome as a function of the main effects of the frequency of these 200 selected codes and treatment. We considered this the true outcome model and used it to create a simulated binary outcome variable (described later). Note that the frequency variables that enter the true outcome-generating model are not available to any of the variable selection methods; all methods relied on categorizations of code frequencies produced by the HDPS algorithm. Also, we did not use any investigator-selected variables in either the simulation setup or analysis since, in this study, we were not interested in evaluating the usefulness of the HDPS beyond adjustment for investigator-specified confounders. We wanted to create settings in which confounding control could be attributed entirely to the described data-adaptive tools being investigated.
We created simulated data sets by sampling, with replacement, 10 000 individuals from the original study cohort. For each sampled individual, we determined the probability of outcome occurrence by putting the covariate values into the fitted true outcome model previously described. We then used these probabilities to simulate a binary outcome for each individual. We selected the intercept value for the outcome model so the overall outcome incidence was 10% (scenario 1 in Table 1). We sampled treated and untreated individuals disproportionately from the original population so that the treatment prevalence within the sampled population was approximately 40%. We simulated under a null treatment effect to avoid complications with the collapsibility of the odds ratio.48
We considered 5 additional scenarios in which we varied the outcome incidence, treatment prevalence, sample size, and treatment effect (Table 1). We simulated 100 data sets for each scenario. For each, we considered 10 methods for modeling the PS:
- HDPS 25: Logistic PS model controlling for 25 HDPS-selected variables
- HDPS 100: Logistic PS model controlling for 100 HDPS-selected variables
- HDPS 200: Logistic PS model controlling for 200 HDPS-selected variables
- HDPS 300: Logistic PS model controlling for 300 HDPS-selected variables
- HDPS 400: Logistic PS model controlling for 400 HDPS-selected variables
- HDPS 500: Logistic PS model controlling for 500 HDPS-selected variables
- HDPS SL: PSs estimated by running the SL on the library of HDPS models (methods 1-6)
- CTMLE 10: CTMLE with HDPS preordering and a patience parameter of 10
- CTMLE 50: CTMLE with HDPS preordering and a patience parameter of 50
- HDPS LASSO: LASSO regression for the outcome using 500 HDPS variables as the predictors. We excluded variables whose coefficients were shrunk to 0. We included all other variables in a logistic PS model.
We used all of these, except for HDPS SL, to identify a subset of HDPS-created variables. We then used these selected variables to fit a logistic PS model, which we used for confounding control. We used HDPS SL to produce a new set of predicted values based on the library of fitted HDPS models. We estimated treatment effects using PS stratification, PS matching, inverse probability treatment weighting (IPTW), and TMLE. For PS stratification, we stratified on deciles of the estimated PSs. We conducted PS matching using 1:1 nearest neighbor caliper matching without replacement and with a caliper distance of 0.25 SDs of the PS distribution.49,50 We implemented TMLE using the fitted PS with an intercept outcome model. While fitting an intercept outcome model does not take advantage of the double robustness of the TMLE method, in this study we were not interested in optimizing the performance of TMLE but were interested in evaluating methods that can complement the HDPS to improve the robustness of PS variable/model selection in high-dimensional covariate settings. When implementing TMLE for scenarios involving rare outcomes, we stabilized the estimate by imposing bounds on the conditional mean of the outcome as described by Balzer et al.51
We evaluated the performance of the described methods by calculating the percentage bias removed and mean squared error (MSE) in the estimated treatment effects. We defined the percentage bias removed as , where RDtrue is the true risk difference, RDadjusted is the adjusted risk difference after implementing a variable selection strategy for confounding control, and RDunadjusted is the unadjusted, or crude, risk difference. In the scenarios involving a non-null treatment effect, we calculated RDtrue by imputing the true potential outcomes for each individual, then using the potential outcomes to calculate the true treatment effect in the treated (used when calculating bias for PS matching) and the true treatment effect in the population (used when calculating bias for PS stratification, IPTW, and TMLE). We calculated the MSE by taking the average of the bias squared across all simulation runs.
Results
Results From Evaluation of Predictive Algorithms in Empirical Examples
Figures 1 and 2 show the computation times for the 23 individual machine learning algorithms and the HDPS algorithm across all 3 data sets without the use of super learner. Computation time is measured in seconds. Figure 1 shows the computation time for the machine learning algorithms that use only baseline covariates. Figure 2 shows the computation time for the HDPS algorithm at varying values of the tuning parameters k and n. The variable n represents the number of variables that the HDPS algorithm considers within each data dimension and k represents the total number of variables that are selected or included in the final HDPS model. The computation time is sensitive to n while less sensitive to k. This suggests most of the computation time for HDPS is spent generating and screening covariates. The computation time of SL is not placed in the figures. SL with baseline covariates takes more than twice as long as the sum of the computation time for each individual algorithm in its library: SL splits data into training and validation sets, fits the base learners on the training set, finds weights based the on the validation set, and finally retrains the model on the whole set. In other words, SL fits every algorithm twice with additional processing time for computing the weights. Therefore, the computation time will be about twice the sum of its constituent algorithms, which is what we see in this study.

Figure 1
Computation Times for Each of the 23 Individual Machine Learning Algorithms.
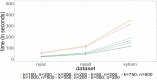
Figure 2
Computation Times for HDPS Algorithms.
Figure 3 shows the negative log likelihood for SLs 1 and 2 and each of the 23 machine learning algorithms (with only baseline covariates). Figure 4 shows the negative log likelihood for HDPS algorithms with varying tuning parameters, n and k. The performance of HDPS is not sensitive to either n or k. In most cases, HDPS outperforms most algorithms in the library as it takes advantage of the extra information from code data. However, in the Vytorin data set there are still some machine learning algorithms that perform slightly better than HDPS with respect to the negative log likelihood. We can see that the SL (without HDPS) outperforms all the other algorithms, empirically verifying the optimal property proved by previous literature.25 The SL can do at least as well as the best algorithm in the library. The figures show that including the HDPS algorithm improves the performance of SL. With the help of HDPS, SL achieves the best performance among all the algorithms.
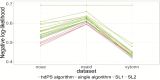
Figure 3
Negative Log Likelihood for SLs 1 and 2.

Figure 4
Negative Log Likelihood for the HDPS Algorithm.
In Figures 3 and 5, we compare the performance of SLs 1 and 2, the HDPS algorithm, and each of the 23 machine learning algorithms. Although we optimized SLs with respect to the negative log likelihood loss function, SL1 and SL2 have outstanding performance with respect to the AUC. Over the NOAC and NSAID data set, SL1 (with only baseline variables) achieves the best AUC compared with all machine learning algorithms in its library, with only a slightly weaker AUC performance than HDPS. In the Vytorin data set, SL1 outperforms HDPS algorithms with respect to AUC, even though the HDPS algorithms use the additional claims data.

Figure 5
AUC for SLs 1 and 2 and Each of the Algorithms.
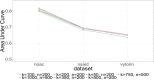
Figure 6
AUC for HDPS Models With Various Tuning Parameters.
Results From the Plasmode Simulations
Figures 7 and 8 show the percentage bias removed and MSE in the estimated treatment effects for each of the 10 variable selection strategies and each data set when stratifying on the estimated PSs. Among the methods that implemented only the HDPS algorithm for variable selection (methods 1-6, previously described), the logistic HDPS model that included 100 variables (HDPS 100) generally performed best in terms of removing bias in the estimated treatment effect with the percentage bias removed ranging from approximately 70% to 98% for the NSAID data, 85% to 99% for the NOAC data, and 84% to 99% for the Vytorin data (Figure 7). As we added more variables to the HDPS model, the bias in the estimated treatment effects tended to increase. The HDPS model that included 500 variables (HDPS 500) generally removed the least amount of bias in the effect estimates with percentage bias removed ranging from 48% to 75%, 67% to 95%, and 59% to 97% for the NSAID, NOAC, and Vytorin data sets, respectively (Figure 7).
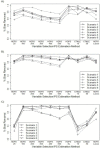
Figure 7
Percentage Bias Removed for Each Scenario and Method When Stratifying on the Estimated PSs.
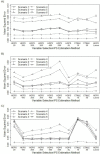
Figure 8
MSE Multiplied by 100 for Each Scenario and Method When Stratifying on the Estimated PSs.
Among the variable selection methods that combined the SL, CTMLE, or LASSO regression with the HDPS (methods 7-10 described previously), the SL tended to be the most consistent with percentage bias removed generally being similar to the best-performing HDPS model. The CTMLE 10 and CTMLE 50 methods were less consistent and performed well for the NSAID and NOAC data sets, but both strategies performed poorly for the Vytorin data set (Figure 7). The HDPS LASSO variable selection method was also less consistent compared with the SL for all 3 data sets (Figure 4). General patterns in bias were similar when treatment effects were estimated through PS matching, IPTW, and TMLE (see Supplemental Figures 1-3 found in the Appendix).
In terms of MSE, there was little difference across the HDPS models (HDPS 25 through HDPS 500) except in settings involving smaller sample sizes (scenario 3 in Figure 8) or reduced treatment prevalence (scenario 5 in Figure 8). For the Vytorin data set, there was an increase in the MSE for HDPS 25 relative to HDPS 100 through 500. In these settings, patterns were similar to Figure 7, with the HDPS 100 model performing best in terms of reduced MSE, while the HDPS 500 model resulted in effect estimates with the largest MSE. Among the variable selection methods that combined the SL, CTMLE, or LASSO regression with the HDPS, combining the HDPS with the SL was the most consistent in terms of reducing MSE in the estimated treatment effects (Figure 8). We observed similar patterns when we estimated treatment effects through PS matching, IPTW, and TMLE (see Supplemental Figures 4-6 found in the Appendix).
To better understand the performance of the CTMLE and LASSO variable selection strategies (methods 8-10 described previously), we plotted the number of variables selected by the CTMLE 10, CTMLE 50, and HDPS LASSO method for the NSAID data set (Figure 9). CTMLE 10 tended to select the fewest variables, followed by CTMLE 50 (Figure 9). We found similar patterns for the NOAC and Vytorin data sets (not shown).

Figure 9
Number of Variables Selected by CTMLE 10, CTMLE 50, and HDPS LASSO for Each Scenario When Using the NSAID Data Set.
The goal of the SL is to minimize a specified loss function, which in this study was the negative log likelihood. To better understand the performance of the SL when combined with the HDPS, we plotted the 10-fold cross-validated negative log likelihood for each of the HDPS models (methods 1-6) and SL (method 7). Figure 10 shows that the SL performed slightly better than the best-performing HDPS model for each scenario and data set. Figure 10 further shows that the greatest variation in the negative log likelihood occurred for the scenarios involving smaller sample sizes, which is likely a consequence of severe overfitting (scenario 3).
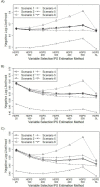
Figure 10
Negative Log Likelihood for Each of the HDPS Models and HDPS SL.
Computation times for methods 7 through 10 are provided in Figure 11. For smaller sample sizes, all methods had similar computation times. As the sample size increased, the computation time for CTMLE 50 increased substantially relative to the methods that combined the SL with HDPS or LASSO regression with HDPS (Figure 11).

Figure 11
Computation Times for CTMLE 10, CTMLE 50, HDPS SL, and HDPS LASSO for Various Sample Sizes in the NSAID, NOAC, and Vytorin Data Sets.
Discussion
In this study, we used plasmode simulations based on published health care database studies to evaluate data-adaptive approaches that can be used in combination with the HDPS to improve confounding control in electronic health care databases. We considered strategies that combined the HDPS with the SL prediction algorithm, a modified CTMLE that is scalable to large data sets, and LASSO regression. While the HDPS is not the only method for variable selection in high-dimensional covariate settings, the focus of this study was to optimize the performance of the HDPS, as it is becoming increasingly used in medical studies using electronic health care databases.
We found that PS models can be sensitive to the number of variables included in the adjustment set, particularly in small samples where overfitting the PS can be severe. In most settings, combining the HDPS with SL prediction modeling avoided severe overfitting of the PS model and tended to be the most robust in terms of reducing bias in the estimated treatment effects. When fitting the SL, we considered only additive logistic models as candidate learners that make strong parametric assumptions. Including interactions when fitting the SL that accommodates the HDPS would be a natural extension of the methods evaluated here and could easily be accommodated. However, we leave the evaluation of these methods within more complex plasmode simulations for future work. In such settings, consideration of more flexible machine learning models when combining the HDPS with SL may further improve performance.38 Methods that combined the HDPS with LASSO regression or the scalable version of CTMLE also performed well for many of the settings considered but tended to be less consistent in terms of reducing bias compared with the combination of the HDPS and SL.
The SL focuses on selecting PS models that are optimal in terms of reducing a cross-validated loss function (eg, the negative log likelihood) for treatment assignment. While this strategy performed well when used in combination with the HDPS, we emphasize that selection rules focusing only on minimizing treatment prediction error are generally not optimal for PS validation. The inclusion of instrumental variables can improve treatment prediction while possibly worsening confounding control.23,42 In this study, we used the HDPS to screen strong instruments before implementing the SL so instrumental variables are not included in the PS model. This should improve the correspondence between treatment prediction and confounding control. We found that the cross-validated negative log likelihood performed well for evaluating PS models in settings where there were large differences in the magnitude of overfitting between the fitted PS models. In settings where differences in overfitting were less severe, this correspondence was less pronounced.
To what extent overfitting impacts the ability of PS models to balance covariates and control for confounding is uncertain. Previous studies have argued that overfitting the PS model may not negatively impact the objectives of the PS and, in some cases, a little overfitting may even be beneficial by removing random imbalances in the data to improve the precision of effect estimates.42 In this study we found that if overfitting became severe there was a correspondence with increased bias and MSE in the estimated treatment effects. However, this correspondence was not perfect and no single method was optimal across all data sets and scenarios. While plasmode simulations allow investigators to evaluate methods in settings that better reflect real-world practice, they also make it difficult to elucidate reasons for observed differences in the performance across methods and are limited to the data sets and scenarios assessed. Further, in this study we did not consider investigator-specified confounders in either the plasmode simulations or analyses. When a substantial proportion of confounding can be captured through investigator-identified confounders, there may be little difference in the performance across various data-adaptive approaches. While data-adaptive approaches for high-dimensional confounder adjustment can help improve the validity of causal inference in medical studies using large health care databases, we emphasize that these tools do not address other important sources of bias that are common in secondary health care databases (eg, data misclassification, informative censoring, missing data, and unmeasured confounding). We emphasize that the greatest gains in study validity will often be gained through expert knowledge, investigator-identified confounders, study design, and other restriction criteria (eg, the new user active comparator design).
Finally, previous studies have established theoretical advantages of the original version of the CTMLE algorithm.26 These studies have shown that the CTMLE has many desirable properties and, in many instances, can outperform other methods for causal estimation.26,29 The modified CTMLE is scalable to large data; however, it is sensitive to the preordering of variables and patience parameter setting. In our work, we considered only a preordering of variables based on the HDPS bias formula and considered patience settings that put strong restrictions on the number of variables the algorithm could consider. We repeated analyses for scenario 1 in the Vytorin data set using the modified CTMLE with a less-restrictive patience setting of 100. This improved confounding control with approximately 57% of the confounding bias removed compared with approximately 43% for HDPS 50. While patience settings that are less restrictive will generally improve the performance of the modified CTMLE algorithm, they can also substantially increase computation time. For scenario 1 in the Vytorin data set, increasing the patience setting from 50 to 100 resulted in more than a 7-fold increase in computation time. More research is needed on how to find the optimal parameter settings and variable orderings when implementing the scalable version of the CTMLE algorithm in large electronic health care data.
Conclusions
In typical health care claims databases with a high-dimensional covariate space of almost exclusively binary indicator terms, there was very little to no improvement in the effect estimation of a variety of strategies above the base-case HDPS. Combined with plasmode simulation study findings and other empirical studies, there is consolidating evidence that HDPS is a robust approach to confounder reduction in claims databases. However, we also conclude that a PS model's ability to control confounding is impacted by the number of variables selected for adjustment and for which severe overfitting can negatively impact the properties of effect estimates. Combining the HDPS variable selection algorithm with SL is a promising strategy for automated data-adaptive PS variable selection in health care database studies and may be particularly useful during early periods of drug approval when small samples and rare exposures are common.
References
- 1.
- Rosamond W, Flegal K, Furie K, et al. American Heart Association statistics C, stroke statistics S. Heart disease and stroke statistics—2008 update: a report from the American Heart Association statistics committee and stroke statistics subcommittee. Circulation. 2008;117(4):e25-e146. [PubMed: 18086926]
- 2.
- Schneeweiss S, Avorn J. A review of uses of health care utilization databases for epidemiologic research on therapeutics. J Clin Epidemiol. 2005;58:323-337. [PubMed: 15862718]
- 3.
- Schneeweiss S. Developments in post-marketing comparative effectiveness research. Clin Pharmacol Ther. 2007;82:143-156. [PMC free article: PMC2905665] [PubMed: 17554243]
- 4.
- Walker AM. Confounding by indication. Epidemiology. 1996;7:335-336. [PubMed: 8793355]
- 5.
- Go AS, Lee WY, Yang J, Lo JC, Gurwitz JH. Statin therapy and risks for death and hospitalization in chronic heart failure. JAMA. 2006;296:2105-2111. [PubMed: 17077375]
- 6.
- Schneeweiss S. A basic study design for expedited safety signal evaluation based on electronic healthcare data. Pharmacoepidemiol Drug Saf. 2010;19:858-868. [PMC free article: PMC2917262] [PubMed: 20681003]
- 7.
- Meier CR, Schlienger RG, Kraenzlin ME, Schlegel B, Jick H. HMG-CoA reductase inhibitors and the risk of fractures. JAMA. 2000;283:3205-3210. [PubMed: 10866867]
- 8.
- Jick H, Zornberg GL, Jick SS, Seshadri S, Drachman DA. Statins and the risk of dementia. Lancet. 2000;356:1627-1631. [PubMed: 11089820]
- 9.
- Tavazzi L, Maggioni AP, Marchioli R, et al. Effect of rosuvastatin in patients with chronic heart failure (the GISSI-HF trial): a randomised, double-blind, placebo-controlled trial. Lancet. 2008;372:1231-1239. [PubMed: 18757089]
- 10.
- Kjekshus J, Apetrei E, Barrios V, et al. Group C. Rosuvastatin in older patients with systolic heart failure. N Engl J Med. 2007;357:2248-2261. [PubMed: 17984166]
- 11.
- Sturmer T, Joshi M, Glynn RJ, Avorn J, Rothman KJ, Schneeweiss S. A review of the application of propensity score methods yielded increasing use, advantages in specific settings, but not substantially different estimates compared with conventional multivariable methods. J Clin Epidemiol. 2006;59:437-447. [PMC free article: PMC1448214] [PubMed: 16632131]
- 12.
- Schneeweiss S. Understanding secondary databases: a commentary on “sources of bias for health state characteristics in secondary databases.” J Clin Epidemiol. 2007;60:648-650. [PMC free article: PMC2905674] [PubMed: 17573976]
- 13.
- Bross ID. Spurious effects from an extraneous variable. J Chronic Dis. 1966;19:637-647. [PubMed: 5966011]
- 14.
- Schneeweiss S. Sensitivity analysis and external adjustment for unmeasured confounders in epidemiologic database studies of therapeutics. Pharmacoepidemiol Drug Saf. 2006;15:291-303. [PubMed: 16447304]
- 15.
- Gagne JJ, Fireman B, Ryan PB, et al. Design considerations in an active medical product safety monitoring system. Pharmacoepidemiol Drug Saf. 2012;21(Suppl 1):32-40. [PubMed: 22262591]
- 16.
- Rassen JA, Glynn RJ, Brookhart MA, Schneeweiss S. Covariate selection in high-dimensional propensity score analyses of treatment effects in small samples. Am J Epidemiol. 2011;173:1404-1413. [PMC free article: PMC3145392] [PubMed: 21602301]
- 17.
- Wyss R, Sturmer T. Commentary: balancing automated procedures for confounding control with background knowledge. Epidemiology. 2014;25:279-281. [PMC free article: PMC4110964] [PubMed: 24487210]
- 18.
- Methodology Committee of the Patient-Centered Outcomes Research Institute (PCORI). Methodological standards and patient-centeredness in comparative effectiveness research: the PCORI perspective. JAMA. 2012;307:1636-1640.
- 19.
- Schneeweiss S, Rassen JA, Glynn RJ, Avorn J, Mogun H, Brookhart MA. High-dimensional propensity score adjustment in studies of treatment effects using health care claims data. Epidemiology. 2009;20:512-522. [PMC free article: PMC3077219] [PubMed: 19487948]
- 20.
- Franklin JM, Eddings W, Glynn RJ, Schneeweiss S. Regularized regression versus the high-dimensional propensity score for confounding adjustment in secondary database analyses. Am J Epidemiol. 2015;182(7):651-659. [PubMed: 26233956]
- 21.
- Rassen JA, Schneeweiss S. Using high-dimensional propensity scores to automate confounding control in a distributed medical product safety surveillance system. Pharmacoepidemiol Drug Saf. 2012;21(Suppl 1):41-49. [PubMed: 22262592]
- 22.
- Guertin JR, Rahme E, LeLorier J. Performance of the high-dimensional propensity score in adjusting for unmeasured confounders. Eur J Clin Pharmacol. 2016;72:1497-1505. [PMC free article: PMC5110594] [PubMed: 27578249]
- 23.
- Myers JA, Rassen JA, Gagne JJ, et al. Effects of adjusting for instrumental variables on bias and precision of effect estimates. Am J Epidemiol. 2011;174:1213-1222. [PMC free article: PMC3254160] [PubMed: 22025356]
- 24.
- Liu W, Brookhart MA, Schneeweiss S, Mi X, Setoguchi S. Implications of M bias in epidemiologic studies: a simulation study. Am J Epidemiol. 2012;176:938-948. [PubMed: 23100247]
- 25.
- van der Laan MJ, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol. 2007;6:Article 25. doi:10.2202/1544-6115.1309 [PubMed: 17910531] [CrossRef]
- 26.
- van der Laan MJ, Gruber S. Collaborative double robust targeted maximum likelihood estimation. Int J Biostat. 2010;6:Article 17. doi:10.2202/1557-4679.1181 [PMC free article: PMC2898626] [PubMed: 20628637] [CrossRef]
- 27.
- Polley EC, Rose S, van der Laan MJ. Super learning. In: van der Laan MJ, Rose S, eds. Targeted Learning: Causal Interference for Observational and Experimental Data. Springer; 2011:43-66.
- 28.
- Gruber S, van der Laan MJ. Targeted maximum likelihood estimation: a gentle introduction. Berkeley Division of Biostatistics working paper 252. August 2009.
- 29.
- Gruber S, van der Laan MJ. An application of collaborative targeted maximum likelihood estimation in causal inference and genomics. Int J Biostat. 2010;6:Article 18. doi:10.2202/1557-4679.1182 [PMC free article: PMC3126668] [PubMed: 21731530] [CrossRef]
- 30.
- Franklin JM, Schneeweiss S, Polinski JM, Rassen JA. Plasmode simulation for the evaluation of pharmacoepidemiologic methods in complex healthcare databases. Comput Stat Data Anal. 2014;72:219-226. [PMC free article: PMC3935334] [PubMed: 24587587]
- 31.
- Schneeweiss S, Eddings W, Glynn RJ, Patorno E, Rassen J, Franklin JM. Variable selection for confounding adjustment in high-dimensional covariate spaces when analyzing healthcare databases. Epidemiology. 2017;28:237-248. [PubMed: 27779497]
- 32.
- Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29-36. [PubMed: 7063747]
- 33.
- Ali MS, Groenwold RH, Pestman WR, et al. Propensity score balance measures in pharmacoepidemiology: a simulation study. Pharmacoepidemiol Drug Saf. 2014;23:802-811. [PubMed: 24478163]
- 34.
- Austin PC. Balance diagnostics for comparing the distribution of baseline covariates between treatment groups in propensity-score matched samples. Stat Med. 2009;28:3083-3107. [PMC free article: PMC3472075] [PubMed: 19757444]
- 35.
- Franklin JM, Rassen JA, Ackermann D, Bartels DB, Schneeweiss S. Metrics for covariate balance in cohort studies of causal effects. Stat Med. 2014;33:1685-1699. [PubMed: 24323618]
- 36.
- Stuart EA, Lee BK, Leacy FP. Prognostic score-based balance measures can be a useful diagnostic for propensity score methods in comparative effectiveness research. J Clin Epidemiol. 2013;66(8 Suppl):S84-S90. doi:10.1016/j.jclinepi.2013.01.013 [PMC free article: PMC3713509] [PubMed: 23849158] [CrossRef]
- 37.
- Rose S. Mortality risk score prediction in an elderly population using machine learning. Am J Epidemiol. 2013;177:443-452. [PubMed: 23364879]
- 38.
- Pirracchio R, Petersen ML, van der Laan M. Improving propensity score estimators' robustness to model misspecification using super learner. Am J Epidemiol. 2015;181:108-119. [PMC free article: PMC4351345] [PubMed: 25515168]
- 39.
- Westreich D, Cole SR, Funk MJ, Brookhart MA, Sturmer T. The role of the c-statistic in variable selection for propensity score models. Pharmacoepidemiol Drug Saf. 2011;20:317-320. [PMC free article: PMC3081361] [PubMed: 21351315]
- 40.
- Weitzen S, Lapane KL, Toledano AY, Hume AL, Mor V. Weaknesses of goodness-of-fit tests for evaluating propensity score models: the case of the omitted confounder. Pharmacoepidemiol Drug Saf. 2005;14:227-238. [PubMed: 15386700]
- 41.
- Wyss R, Ellis AR, Brookhart MA, et al. The role of prediction modeling in propensity score estimation: an evaluation of logistic regression, bcart, and the covariate-balancing propensity score. Am J Epidemiol. 2014;180:645-655. [PMC free article: PMC4157700] [PubMed: 25143475]
- 42.
- Brookhart MA, Schneeweiss S, Rothman KJ, Glynn RJ, Avorn J, Sturmer T. Variable selection for propensity score models. Am J Epidemiol. 2006;163:1149-1156. [PMC free article: PMC1513192] [PubMed: 16624967]
- 43.
- Bhattacharya J, Vogt WB. Do instrumental variables belong in propensity scores? National Bureau of Economic Research technical working paper 343. September 2007.
- 44.
- Pang M, Schuster T, Filion KB, Eberg M, Platt RW. Targeted maximum likelihood estimation for pharmacoepidemiologic research. Epidemiology. 2016;27:570-577. [PMC free article: PMC4890840] [PubMed: 27031037]
- 45.
- Schuler MS, Rose S. Targeted maximum likelihood estimation for causal inference in observational studies. Am J Epidemiol. 2017;185:65-73. [PubMed: 27941068]
- 46.
- Ju C, Gruber S, Lendle SD, et al. Scalable collaborative targeted learning for large scale and high-dimensional data. U.C. Berkeley Division of Biostatistics working paper 352. 2016. https://core
.ac.uk/download /pdf/61322734.pdf - 47.
- Low YS, Gallego B, Shah NH. Comparing high-dimensional confounder control methods for rapid cohort studies from electronic health records. J Comp Eff Res. 2016;5:179-192. [PMC free article: PMC4933592] [PubMed: 26634383]
- 48.
- Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Stat Sci. 1999;14:29-46.
- 49.
- Austin PC. Optimal caliper widths for propensity-score matching when estimating differences in means and differences in proportions in observational studies. Pharmaceutical Stat. 2011;10:150-161. [PMC free article: PMC3120982] [PubMed: 20925139]
- 50.
- Connolly JG, Gagne JJ. Comparison of calipers for matching on the disease risk score. Am J Epidemiol. 2016;183:937-948. [PMC free article: PMC4867154] [PubMed: 27037270]
- 51.
- Balzer L, Ahern J, Galea S, van der Laan M. Estimating effects with rare outcomes and high dimensional covariates: knowledge is power. Epidemiol Methods. 2016;5:1-18. [PMC free article: PMC5436729] [PubMed: 28529839]
- 52.
- Lendle SD. HDPS. GitHub. Published 2016. Accessed June 13, 2019. https://github
.com/lendle/hdps - 53.
- Lendle SD. TargetedLearning. GitHub. Published 2016. Accessed June 13, 2019. https://github
.com/lendle /TargetedLearning.jl
Supplemental Table
Table 3
Simulation Scenarios.
Acknowledgment
Research reported in this report was [partially] funded through a Patient-Centered Outcomes Research Institute® (PCORI®) Award (#ME-1303-5638) Further information available at: https://www.pcori.org/research-results/2013/methods-improving-confounding-control-comparative-effectiveness-research-using
Appendices
Appendix 1.
Overview of TMLE, Greedy CTMLE, and Scalable CTMLE (PDF, 543K)
Appendix 2.
Description of Study Cohorts Used in Plasmode Simulations (PDF, 337K)
Appendix 3.
Imputing Potential Outcomes From Simulated Data (PDF, 386K)
Appendix 4.
Supplemental Figures (PDF, 921K)
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Statin datasets, respectively.
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Statin datasets, respectively.
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Statin datasets, respectively.
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Vytorin datasets, respectively.
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Vytorin datasets, respectively.
Plots A, B, and C show results for plasmode simulations based on the NSAID, NOAC, and Vytorin datasets, respectively.
Suggested citation:
Wyss R, Schneeweiss S, van der Laan M, Lendle SD, Ju C, Franklin JM. (2019). Methods for Improving Confounding Control in Comparative Effectiveness Research Using Electronic Healthcare Databases. Patient-Centered Outcomes Research Institute (PCORI). https://doi.org/10.25302/7.2019.ME.13035638
Disclaimer
The [views, statements, opinions] presented in this report are solely the responsibility of the author(s) and do not necessarily represent the views of the Patient-Centered Outcomes Research Institute® (PCORI®), its Board of Governors or Methodology Committee.
- NLM CatalogRelated NLM Catalog Entries
- PMCPubMed Central citations
- PubMedLinks to PubMed
- Using Super Learner Prediction Modeling to Improve High-dimensional Propensity Score Estimation.[Epidemiology. 2018]Using Super Learner Prediction Modeling to Improve High-dimensional Propensity Score Estimation.Wyss R, Schneeweiss S, van der Laan M, Lendle SD, Ju C, Franklin JM. Epidemiology. 2018 Jan; 29(1):96-106.
- Propensity score prediction for electronic healthcare databases using Super Learner and High-dimensional Propensity Score Methods.[J Appl Stat. 2019]Propensity score prediction for electronic healthcare databases using Super Learner and High-dimensional Propensity Score Methods.Ju C, Combs M, Lendle SD, Franklin JM, Wyss R, Schneeweiss S, van der Laan MJ. J Appl Stat. 2019; 46(12):2216-2236. Epub 2019 Feb 22.
- High-dimensional propensity score algorithm in comparative effectiveness research with time-varying interventions.[Stat Med. 2015]High-dimensional propensity score algorithm in comparative effectiveness research with time-varying interventions.Neugebauer R, Schmittdiel JA, Zhu Z, Rassen JA, Seeger JD, Schneeweiss S. Stat Med. 2015 Feb 28; 34(5):753-81. Epub 2014 Dec 8.
- Review Methods for Variable Selection and Treatment Effect Estimation in Nonrandomized Studies with Few Outcome Events and Many Confounders[ 2018]Review Methods for Variable Selection and Treatment Effect Estimation in Nonrandomized Studies with Few Outcome Events and Many ConfoundersFranklin JM, Eddings W, Gopalakrishnan C, Glynn RJ, Austin PC, Stuart EA, Schneeweiss S. 2018 Mar
- Review Automated data-adaptive analytics for electronic healthcare data to study causal treatment effects.[Clin Epidemiol. 2018]Review Automated data-adaptive analytics for electronic healthcare data to study causal treatment effects.Schneeweiss S. Clin Epidemiol. 2018; 10:771-788. Epub 2018 Jul 6.
- Methods for Improving Confounding Control in Comparative Effectiveness Research ...Methods for Improving Confounding Control in Comparative Effectiveness Research Using Electronic Healthcare Databases
Your browsing activity is empty.
Activity recording is turned off.
See more...
