This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs License which permits noncommercial use and distribution provided the original author(s) and source are credited. (See https://creativecommons.org/licenses/by-nc-nd/4.0/
NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Structured Abstract
Background:
Appropriate causal inference methods are required for comparative effectiveness research to produce valid and relevant findings from observational data. Two prominent classes of such methods are based on unconfoundedness or instrumental variable (IV) assumptions. Although extensive research has been done, it remains highly challenging to estimate propensity scores (PSs) and regression functions and to perform subsequent inference about average treatment effects (ATEs). The conventional approach employs an iterative process of model building and fitting, depending on ad hoc modeling choices, where statistical uncertainty is difficult to quantify. Recently, various methods have been proposed that apply off-the-shelf machine learning algorithms but either ignore statistical inference or invoke strong smoothness assumptions to justify consistent estimation of regression functions and subsequent statistical inference about treatment effects.
Objectives:
The objective of our research is to develop and evaluate a new set of statistically rigorous, numerically tractable, and pragmatic methods for drawing inferences about ATEs using PSs or IVs, while fitting PS and regression models with a large number of regressors.
Methods:
We propose regularized calibrated estimation and model-assisted inferences about ATEs under the assumption of no unmeasured confounding or local ATEs under IV assumptions in high-dimensional settings. We derived numerical algorithms to implement the methods, conducted simulation studies to evaluate the methods, and investigated empirical applications of the proposed methods, compared with existing methods.
Results:
The proposed methods are shown to yield valid statistical inference (ie, CIs and hypothesis testing) about treatment parameters under weak technical conditions in high-dimensional settings. Simulation studies and empirical applications demonstrate the advantages of the proposed methods compared with related methods.
Conclusions:
We developed new statistical methods and theory using PSs or IVs for causal inference. Using the proposed methods, PS and regression models can be fitted with a possibly large number of regressors, including main effects and interactions of the covariates, and CIs, and hypothesis tests can be obtained about treatment effects in a numerically tractable and statistically principled manner. Our methods are implemented in the publicly released R package RCAL.
Limitations:
Currently used methods handle cross-sectional studies and assume that the treatment and instrument are binary. It is desirable to extend our methods to handle multivalued treatments and instruments and to analyze longitudinal and survival data.
Background
Causal Inference
PCORI was established with the mission to help patients, clinicians, and other health care stakeholders make better-informed health care decisions and improve health care delivery and outcomes. One of the most frequently sought types of information is whether a specific treatment will cause deterioration or improvement in the outcomes of interest compared with other treatments. To provide such information, it is important to conduct comparative effectiveness research (CER). However, a fundamental challenge in nonrandomized, observational studies is that it can be enormously difficult to disentangle the effects of the treatment from other risk factors, known as confounding variables (or covariates), which might influence the health outcomes and, at the same time, vary between patients who had the intervention treatment and those who had the comparator treatment. The subject of how to address confounding and draw inferences about treatment effects is broadly called causal inference, spanning multiple disciplines, including epidemiology, econometrics, and statistics.
As discussed in the PCORI Methodology Report (PCORI Methodology Committee, 2021), Section III (8), appropriate causal inference methods are required for CER to produce valid and relevant findings from observational data, where treatment choices are self-selected rather than randomly assigned. There is extensive literature on various analytical methods for causal inference (Morgan & Winship 2014; van der Laan & Robins 2003). The PCORI Methodology Report explicitly mentions 2 methods, propensity scores (PSs) (Rosenbaum & Rubin 1983) and instrumental variables (IVs) (Angrist et al. 1996; Hernan & Robins 2006), as being “relatively well-developed and increasingly used in CER.” The Methodology Report provides the following standards for the use of these 2 methods:
- CI-5. Report the assumptions underlying the construction of propensity scores and the comparability of the resulting groups in terms of the balance of covariates and overlap.
- CI-6. Assess the validity of the instrumental variable (ie, how the assumptions are met) and report the balance of covariates in the groups created by the instrumental variable.
The PS in CI-5 is defined as the conditional probability of receiving the treatment given covariates (Rosenbaum & Rubin 1983). For IV analysis (CI-6), the conditional probabilities of the instrument given covariates (called IV PSs) can also be used to achieve covariate balance between instrument groups (Tan 2006b, 2010b).
Underlying the preceding standards, however, are at least 2 nontrivial statistical tasks: first, estimating PSs (or IV PSs), and then using the estimated PSs to conduct inferences about treatment effects. In fact, the exact PSs in an observational study are unknown and need to be estimated from empirical data, depending on a PS model, often specified in the form of logistic regression, where the response variable is treatment status and the regressors may include main effects, nonlinear terms, or interactions of the covariates. How such PS models are built and fitted can have a substantial impact on subsequent estimation of treatment effects. In particular, inverse probability weighted (IPW) estimation using PSs may perform poorly even when the PS model appears to be nearly correct (Kang & Schafer 2007). Moreover, statistical uncertainty from model building and fitting for estimating PSs must be properly taken into account when conducting inferences (including CIs and hypothesis tests) about treatment effects.
To mitigate possible misspecification of PS models, researchers can use doubly robust estimation by combining both a PS model and an outcome regression (OR) model, where the response variable is the outcome of interest, and the regressors may include main effects, nonlinear terms, or interactions of the covariates, similar to the PS model. For example, various doubly robust estimators for the average treatment effect (ATE) have been derived in the form of an augmented IPW estimator (Robins et al. 1994; Tan 2006a, 2010a). In theory, a doubly robust estimator remains consistent (ie, unbiased in large samples) if either the PS model or the OR model is correctly specified. In practice, all models used are only approximations to some extent. Hence, the performance of doubly robust methods still depends on how PS and OR models are built and fitted.
Gaps in Existing Methods
Per the preceding discussion, applications of PS and IV methods for estimating treatment effects involve statistical modeling and estimation of PSs and OR functions from empirical data, in addition to the fact that certain structural assumptions are required for the identification of treatment effects at the population level. Moreover, statistical uncertainty from such modeling and estimation must be properly incorporated to obtain valid CIs and hypothesis tests about treatment effects. Below, we outline various limitations in existing methods.
From the perspective of model building for PSs and OR, existing methods suffer broadly from 3 types of limitations:
- Some methods resort to simple models, for example, on OR PSs with main effects of the covariates only, and hence are susceptible to model misspecification.
- Some methods employ an iterative process of model building and fitting (McCullagh & Nelder 1989; Rosenbaum & Rubin 1984), depending on ad hoc modeling choices about nonlinear and interaction terms of the covariates, where statistical uncertainty is difficult to quantify in subsequent inferences about treatment effects.
- Some methods apply off-the-shelf machine learning algorithms, such as random forests or boosted machines (Hastie et al. 2009; McCaffrey et al. 2004), but either ignore statistical inference or invoke strong smoothness assumptions to justify consistent estimation and statistical inference (Chernozhukov et al. 2018).
These limitations are aggravated in high-dimensional settings, with either a large number of covariates (even with main effects only) or a large number of possible nonlinear and interaction terms for even a moderate number of covariates.
To perform model fitting for PSs and outcome regression, existing methods mainly use maximum likelihood or variants as in conventional predictive modeling, regardless of the roles of the fitted functions in the stage of estimating treatment effects. In particular, PS models are often fitted as logistic regression by maximum likelihood (Rosenbaum & Rubin 1984). However, as increasingly realized among practitioners, the purpose of estimating PSs is not primarily to predict treatment status, but to balance risk factors for the outcome across treatment groups to control for measured confounders (Weitzen et al. 2004; Westreich et al. 2011; Wyss et al. 2014). Hence, there is a disconnection between model fitting (ie, parameter estimation) and model evaluation: the parameters of logistic regression are estimated by the predictive criterion of maximum likelihood, but the adequacy of the fitted model is evaluated in terms of covariate balance achieved.
The preceding viewpoint about model fitting is in consonance with recent methodological developments on PSs, including a logistic calibration weighting method (Folsom 1991) and related methods (Kim & Haziza 2014; Vermeulen & Vansteelandt 2015), a calibrated likelihood method (Tan 2010a), and covariate-balancing PSs (Imai & Ratkovic 2014). All of these methods can be seen to address the issue of model fitting in classical, low-dimensional settings, in providing a different way from maximum likelihood to estimate PSs or, equivalently, the IPWs. However, the fundamental issue of model building (ie, how to build a PS model) remains open and challenging, especially in cases with a limited number of observations but a large number of regressors (including nonlinear and interaction terms of the covariates).
Specific Aims
The objective of our research is to develop and evaluate a new set of statistically rigorous, numerically tractable, and practically useful methods using PSs and IVs for estimating treatment effects. We build on a strong track record of working on theory, methods, and applications of PSs and IVs (eg, Tan 2006a b, 2010a b c; Winterstein et al. 2012; Huybrechts et al. 2013; Gerhard et al. 2014), and exploit related ideas in high-dimensional statistical theory and methods, including least absolutely shrinkage and selection operator (Lasso) regularized estimation (Tibshirani 1996) and debiased inferences (Zhang & Zhang 2014; van de Geer et al. 2014; Javanmard & Montanari 2014).
The specific aims of our research are as follows:
- Aim 1. Develop new statistical theory and methods for estimating PSs and for drawing inference about treatment effects from observational data, with possibly a large number of covariates or regressors.
- Aim 2. Develop new statistical theory and methods using IVs for drawing inferences about treatment effects from observational data, with possibly a large number of covariates or regressors.
- Aim 3. Develop and disseminate user-friendly software, including accessible and transparent documentation, for implementation of the new methods.
Significance
The methodological significance of our research is to develop new methods that will substantially improve on existing methods in removing or alleviating the methodological limitations mentioned in the “Gaps in Existing Methods” section above.
- Our approach allows flexible models, prespecified with a possibly large number of regressors, such as main effects and interactions of the covariates, and employs sparsity-inducing regularized estimation to facilitate model selection in a numerically tractable and statistically principled manner.
- Our approach employs calibrated estimation, where the loss functions used in fitting PS and OR models are carefully chosen such that valid inferences can be obtained about treatment parameters while accommodating possible model misspecification. For fitting PS models, calibrated estimation directly induces covariate balancing.
- Our approach is potentially applicable to a variety of causal inference tasks, including inferences about treatment effects using PSs under unconfoundedness or using IVs under the corresponding assumptions.
Regarding the applied significance, our research is expected to have substantial and wide-ranging impact on CER by facilitating practical implementation of PS and IV methods for causal inference, as mentioned in the PCORI Methodology Report. The methods and software developed can be widely applied in various CER studies to increase the transparency, validity, and accuracy of the estimates of treatment effects, in reducing the bias and variation associated with ad hoc model building or over-optimistic machine learning. As such, the proposed methods are critical in providing patients, clinicians, and other health care stakeholders with the information needed to make better-informed health care decisions and improve health care delivery and outcomes.
Changes in the Research Strategy
There were 2 main changes in the research strategy. First, the statistical approach described in the original research proposal involves combining boosting or additive learning (Schapire & Freund 2012; Buhlmann & Hothorn 2007; Friedman et al. 2009) and calibrated estimation (Folsom 1991; Tan 2010a). This approach deals with mainly estimation of PSs and IV PSs, but the issue of conducting valid inferences after PS estimation is not addressed.
During the research, we decided to pursue the approach of combining Lasso regularized estimation and calibrated estimation, which not only facilitates model selection in a numerically tractable manner when building and fitting PS and regression models but also makes it possible to derive model-assisted inferences (including CIs and hypothesis tests) about treatment effects in high-dimensional settings. In other words, we believe that the current methods developed in our research are statistically and numerically more satisfactory than those originally suggested in the application for funding.
Second, the original research proposal included empirical applications, using PSs or IVs, to the then-ongoing PCORI project, “Comparative Effectiveness of Adaptive Pharmacotherapy Strategies for Schizophrenia.” That study, which is now completed (Stroup et al. 2019), compared the effectiveness of 4 alternative medication strategies beyond antipsychotic monotherapy (addition of a second antipsychotic, an antidepressant, a mood stabilizer, or a benzodiazepine) for people diagnosed with schizophrenia. Health outcomes included times to psychiatric hospitalization, cardiovascular events, and death. However, the current methods developed in our research assume that the treatment is dichotomous and the outcomes of interest are fully observed (hence excluding possibly censored survival data). Although effort has been made to investigate survival analysis in our new approach (Tan 2019) as part of the modified contract, a fully developed method is beyond the scope of the current project. Hence, we conducted empirical applications using 2 existing observational studies, with Connors et al (1996) using PSs and Card (1995) using IVs; these are among the example studies often used in the related literature to evaluate new methods for causal inference.
Patient and Stakeholder Engagement
Our stakeholder committee includes Chacku Mathai, director of the Support, Technical Assistance, and Resources (STAR) Center of the National Alliance on Mental Illness; Mark Olfson, professor in the department of psychiatry, College of Physicians and Surgeons, Columbia University; Elizabeth Stuart, professor in the departments of mental health, biostatistics, and health policy and management, Johns Hopkins Bloomberg School of Public Health; and Almut Winterstein, professor in the department of pharmaceutical outcomes and policy, College of Pharmacy, University of Florida. Hence, the stakeholder team is multidisciplinary, with members ranging from biostatisticians to clinical researchers.
During the project period, we met with the stakeholder committee via teleconferences every 9 months and discussed methods and results via emails, with additional interactions on an as-needed basis. We received constructive comments and suggestions from the stakeholder consultants, which led to improvements in various aspects of the research, including comparison of the new and existing methods, presentation and interpretation of the results, applications of the methods, and the utility and user interface of the software.
Our research is primarily centered on statistical methods and theory. Through our engagement with the broader stakeholder communities, we understand better the needs in CER and are learning to focus our methods on addressing meaningful issues from practical perspectives. We also improve communication of the technical aspects of the methodology in nontechnical, substantive terms.
Propensity Scores and Unconfounded Estimation
Setup
Suppose that a simple random sample of n patients is available from a population under study. The observed data consist of independent and identically distributed observations {(Ti, Yi, Xi):I = 1,…,n}, where Ti is a dichotomous treatment (Ti = 1 if treated or Ti = 0 otherwise), Yi is an outcome variable, and Xi = (X1i, …,Xpi) is a collection of measured covariates. In the potential outcomes framework for causal inference (Neyman 1923; Rubin 1974), 2 potential outcomes (, ) are defined on each patient to indicate what the response would be under treatment 0 or 1, respectively. By consistency, the observed outcome Yi is assumed to be either or , depending on whether Ti = 0 or Ti = 1. Two causal parameters commonly studied in CER are the ATE, defined as E(Y1 − Y0) = μ1 − μ0, with μt = E(Yt), and the ATE on the treated (ATT), defined as E(Y1 − Y0 |T = 1). For concreteness, we mainly discuss estimation of ATE.
For causal inference, a fundamental difficulty in estimating ATEs is that for each patient, only 1 potential outcome, Y0 or Y1, is revealed as the observed outcome, and the other is missing (Holland 1986). Nevertheless, the ATE can be identified from the observed data under the 2 assumptions:
- Unconfoundedness: T and (Y0, Y1) are conditionally independent given X (Rubin 1976)
- Overlap (or positivity): 0 < π*(X) < 1, where π*(X) = P(T = 1|X) is called the PS (Rosenbaum & Rubin 1983)
Under these assumptions, there are broadly 2 modeling approaches for estimating ATE.
One approach is to build a regression model for the OR function mt* (X) = E (Y|T = t, X):
where ψ(∙) is an inverse link function; g0 (X) and g1 (X) are vectors of known functions of X, allowed to include nonlinear and interaction terms; and (α0, α1) are vectors of unknown parameters. Let () be the least-squares or maximum quasi-likelihood estimators of (α0, α1), and let . If OR model (1) is correctly specified, then μt = E(Yt) can be consistently estimated by a substitution estimator, for t = 0, 1.
An alternative approach is to build a regression model for the PS, π*(X) = P(T = 1|X) (Rosenbaum & Rubin 1983):
where Π(∙) is an inverse link function; f(X) is a vector of known functions of X, allowed to include nonlinear and interaction terms; and γ is a vector of unknown parameters. Let be the maximum likelihood estimator of γ. Various methods have been proposed to estimate ATEs by matching, stratification, or weighting on the fitted PS . We focus on IPW, which is central to rigorous theory of statistical estimation for causal inference and missing-data problems (eg, Tsiatis 2006). Two standard IPW estimators for μ1 are
Similarly, 2 standard IPW estimators for μ0 are
If PS model (2) is correctly specified, then these IPW estimators are asymptotically valid as the sample size n increases to ∞. However, if PS model (2) is misspecified, the IPW estimators can perform poorly. Even when the PS model is correct or mildly misspecified, inverse weighting can be instable due to estimated PSs close to 0 or 1 (eg, Kang & Schafer 2007).
To attain consistency for the mean μt, the OR estimator or the IPW estimator relies on correct specification of OR model (1) or PS model (2), respectively. In contrast, there are doubly robust estimators depending on both OR and PS models in the augmented IPW form, which for μ1 reads as follows:
where and are fitted values of m1*(X) and π*(X), respectively, and
For example, the augmented IPW estimator used by Robins et al (1994) is , using the fitted values and from maximum (quasi-)likelihood estimation. See Kang & Schafer (2007) and Tan (2007, 2010a) for reviews in low-dimensional settings.
In high-dimensional settings, Belloni et al (2014) and Farrell (2015) studied the estimator using the fitted values and from Lasso regularized maximum likelihood (RML) estimation or similar methods. Their results are mainly of 2 types, each under suitable conditions. The first type shows double robustness: remains consistent if either OR model (1) or PS model (2) is correctly specified. The second type establishes valid CIs: admits the asymptotic expansion
if both OR model (1) and PS model (2) are correctly specified. To address the gap between these results, it is desirable to develop new methods that lead to valid CIs without requiring both OR and PS models to be correctly specified.
There has been a large, growing literature on causal inference related to our work, in addition to work from Belloni et al (2014) and Farrell (2015). Examples include Robins et al (2017), Chernozhukov et al (2018), Smucler et al (2019), van der Laan et al (2019), Ning et al (2020), Dukes and Vansteelandt (2021), Hirschberg and Wager (2021), and Bradic et al (2021). See Tan (2020a, 2020b) and Ghosh and Tan (2020) for further discussion.
PSs and IPW Estimation
Note: The material in this section is adapted from Tan Z. Regularized calibrated estimation of propensity scores with model misspecification and high-dimensional data. Biometrika. 2020;107;137-158.
We developed regularized calibrated estimation for fitting PS models in high-dimensional settings. For concreteness, assume that PS model (2) is a logistic regression model:
where f(x) = {1, f1 (x), …, fp (x)}T is a vector of known functions including the constant, and γ = (γ0, γ1, …, γp)T is a vector of unknown coefficients. The maximum likelihood estimator is defined as a minimizer of the likelihood loss
or, equivalently, as a solution to the score equation
Alternatively, calibrated estimation uses a system of estimating equations such that the weighted averages of the covariates in the treated subsample are equal to the simple averages in the overall sample. The calibrated estimator is defined as a solution to
Interestingly, the estimator can be equivalently defined as a minimizer of the following loss function, called the calibration loss:
Moreover, ℓCAL (γ) is convex in γ and is strictly convex and bounded from below under a certain nonseparation condition (Tan 2020a). The preceding idea of calibrated estimation and similar methods have been studied, and sometimes independently (re)derived, in various contexts of causal inference, missing-data problems, and survey sampling (eg, Folsom 1991; Tan 2010a; Graham et al. 2012; Hainmueller 2012; Imai & Ratkovic 2014; Kim & Haziza 2014; Vermeulen & Vansteelandt 2015; Chan et al. 2016).
To compare calibrated and likelihood estimation, we establish a new relationship between the loss functions ℓCAL (γ) and ℓML (γ). To allow for misspecification of PS model (8), we write ℓML (γ) = κML (γTf) and ℓCAL (γ) = κCAL (γTf), where for a function g(x),
Then, κML (g*) and κCAL (g*) are well defined for the true log odds ratio g*(x) = log[π*(x)/{1-π* (x)}], even when PS model (8) is misspecified, that is, when g*(x) is not of the form γT f(x). For 2 probabilities, ρ ∈ (0, 1) and ρ′∈ (0,1), the Kullback-Leibler divergence is
In addition, let K(ρ,ρ′) = ρ′/ρ – 1 − log(ρ′/ρ), which is strictly convex in ρ′/ρ, with a minimum of 0 at ρ′/ρ = 1. Then Tan (2020a, Proposition 1) shows that
Hence, minimizing the expected calibration loss in γ involves reducing both the expected likelihood loss E [L{π(X;γ), π*(X)}] and an additional term E [K{π(X; γ), π*(X)}], which can be related to the mean squared relative error (MRSE) between π(X; γ) and π*(X):
This measure of relative errors in PSs governs the mean squared error (MSE) of the IPW estimator, , where . The following result was obtained by Tan (2020a, Proposition 2):
Suppose that E[(Y1)2] ≤ c and π*(X) ≥ δ for some constants c > 0 and δ ∈ (0,1).
- If π(X; γ) ≥ a π*(X) for some constant a ∈ (0,1/2), then(11)The factor 5/(3a) in general cannot be improved up to a constant, independent of a.
- If π(X; γ) ≥ b for some constant b ∈ (0,1), then(12)The factor 1/(2b2) in general cannot be improved up to a divisor of order log(b−1).
The expected calibration loss is inflated in (11) by a leading factor 5/(3a), which remains bounded from above as long as a is bounded away from 0, even when some PSs π(X; γ) are close to 0. In contrast, the expected likelihood loss is inflated in (12) by a leading factor 1/(2b2), which may be arbitrarily large when some PSs π(X; γ) are close to 0. This result demonstrates that the minimization of the expected calibration loss controls the MRSE of PSs more strongly than does the expected likelihood loss. See Tan (2020a), Section 3.2, for further discussion.
The preceding discussion compares calibrated and likelihood estimation through their loss functions. Next, we propose a regularized calibrated estimator of γ in PS model (8). There are 2 motivations. First, regularization is needed in the situation where does not exist because the calibration loss (10) is unbounded from below. In our numerical study (Tan 2020a), nonconvergence was found, for example, in 100% of repeated simulations with n = 200 and p = 50. Second, regularization is also needed in high-dimensional settings where the dimension of the regressor vector f (X) is close to or greater than the sample size.
The regularized calibrated estimator, denoted by , is defined by minimizing the calibration loss ℓCAL (γ) with a Lasso penalty (Tibshirani 1996):
where γ1:p = (γ1, …, γp)T excluding the intercept γ0, ∥⋅∥1 denotes the L1 norm such that , and λ ≥ 0 is a tuning parameter. By the Karush-Kuhn-Tucker (KKT) condition for minimization of (13), the fitted PSs, , satisfies
The equality holds in (15) for any j such that the jth estimate is nonzero. The weighted average of each covariate fj(Xi) over the treated group may differ from the overall average of fj(Xi) by no more than λ. In other words, introducing the Lasso penalty to calibrated estimation yields a relaxation of the equalities (9) to box constraints (15). Moreover, by (14), the IPWs, with Ti = 1, sum to the sample size n. Then, the 2 resulting IPW estimators, and , obtained from (3) with replaced by , are identical to each other.
We present a novel algorithm for computing the proposed estimator , that is, minimizing ℓRCAL (γ) in (13) for any fixed λ. The basic idea of the algorithm is to iteratively form a quadratic approximation to the calibration loss ℓCAL (γ) in (10) and solve a Lasso-penalized weighted least-squares problem, similar to existing algorithms for Lasso-penalized maximum likelihood–based logistic regression (eg, Friedman et al. 2010). However, we construct a suitable quadratic approximation after an additional step of replacing certain sample quantities with model expectations. This idea is known as Fisher scoring and was previously used to derive the iterative reweighted least-squares method for fitting generalized linear models with noncanonical links, such as probit regression (McCullagh & Nelder 1989). Moreover, to reduce computational cost, we exploit the majorization-minimization technique (Wu & Lange 2010; Bohning & Lindsay 1988) in solving the Lasso-penalized weighted least-squares problem. See Tan (2020a), Section 4.2, for a detailed discussion.
We provide a theoretical analysis of the regularized calibrated estimator and the resulting IPW estimator of μ1, allowing for misspecification of PS model (8), in high-dimensional settings where the number of regressors in f(X) is close to or greater than the sample size. Our analysis requires a sparsity assumption that only a small but unknown subset (relative to the sample size) of “significant” regressors is associated with nonzero coefficients. Such assumptions are commonly made in high-dimensional regression, where Lasso-type-penalized estimation can theoretically be shown to achieve nearly as small errors of estimation as in oracle estimation, where those significant regressors were known and only those were included in the regression model (eg, Buhlmann & van de Geer 2011). Heuristically, sparsity-based methods and theory, including ours, can be motivated according to the “bet on sparsity” principle: “Use a procedure that does well in sparse problems, since no procedure does well in dense problems” (Hastie et al. 2015).
Our analysis of Lasso-penalized M-estimators deals with the convergence of the estimators, , to their target values under model misspecification, which is related to but distinct from previous results on excess prediction errors (eg, Buhlmann & van de Geer 2011). Moreover, our analysis of , the IPW estimator of μ1 based on , carefully exploits the results described earlier on the calibration loss ℓCAL (γ) to obtain convergence under weaker conditions than previously realized. Our results show that the squared difference is of the order
provided that is sufficiently small, for example, tends to 0 as n and p increase, where s denotes the sparsity size of , that is, the number of nonzero elements in . See Tan (2020a, Section 4.3) for a detailed discussion.
So far, our theory and methods have focused mainly on the estimation of μ1, but they can be directly extended to an estimation of μ0, and hence the ATE, μ1 − μ0. For estimation of μ0 with PS model (8), the calibrated estimator of γ, denoted by , is defined as a solution to
By exchanging T with 1 − T and exchanging γ with − γ in (10), the corresponding loss function minimized by is
For fixed λ ≥ 0, the regularized calibrated estimator is defined as a minimizer of
The fitted PS, , then satisfies (14) and (15) with Ti replaced by 1 − Ti and replaced by , and similar interpretations apply as discussed previously. The resulting IPW estimator of μ0 is , obtained from (4) with replaced by , and that of μ1 − μ0 is .
An interesting feature of our approach is that 2 different estimators of the PS are used when estimating μ1 and μ0. The estimators and may in general have different asymptotic limits when PS model (8) is misspecified, even though their asymptotic limits coincide when model (8) is correctly specified. Such possible differences should not be of concern: the 2 estimators and are decoupled, involving 2 disjoint subsets of fitted PSs on the treated {i: Ti = 1} and the untreated {i: Ti = 0}, respectively. In fact, separate estimation of PSs and inverse probability weights for the treated and untreated samples can lead to more flexible approximations, and hence potentially less bias in the presence of model misspecification. Furthermore, the discovery of whether substantial differences exist between these separately fitted PSs can be used for diagnosis of the validity of model (8). See Chan et al (2016, Section 2.3) for a related discussion.
The proposed method for estimating PSs is implemented as part of the publicly released R package RCAL (Tan & Sun 2020). The implementation is based on the Fisher scoring descent algorithm in Tan (2020a). At the low level, the least-squares Lasso problem is solved using a variation of the active set algorithm, which enjoys a finite termination property (Osborne et al. 2000; Yang & Tan 2018).
Model-Assisted and Doubly Robust Inferences
Note: The material in this section is adapted from Tan Z. Model-assisted inference for treatment effects using regularized calibrated estimation with high-dimensional data. Ann Statist. 2020;48:811-837.
We develop new methods and theory in high-dimensional settings to obtain not only doubly robust point estimators for ATEs, which remain consistent if either a PS model or an OR model is correctly specified, but also model-assisted CIs, which are valid when the PS model is correctly specified but the OR model may be misspecified.
The development in the “PSs and IPW Estimation” section only involves estimating PSs and applying the IPW estimators. To mitigate possible misspecification of PS models and facilitate constructing CIs, we use a doubly robust estimator of μ1 in the augmented IPW form (5), depending on both a PS model and an OR model. There are 2 motivations, in theory. First, the double-robustness property ensures consistency of point estimation even when 1 of the OR and PS models is misspecified. Second, more importantly in high-dimensional settings, augmented IPW estimation makes it possible to establish a simple asymptotic expansion of the resulting estimator such that valid and numerically tractable CIs can be obtained for μ1. In contrast, obtaining valid CIs is difficult based on IPW estimation only, due to penalized estimation in high-dimensional settings, even when the PS model is correctly specified.
To focus on main ideas, consider a logistic PS model (8) as in the “PSs and IPW Estimation” section and a linear OR model,
where , of the same dimension as γ. That is, OR model (1) is specified with the identity link and the regressor vector g1 (X) is the same as f (X) in PS model (2). This condition can be satisfied possibly after enlarging model (1) or (2) to reach the same dimension. Our point estimator of μ1 is
where φ () is defined in (6), with the regularized calibrated estimator as in the “PSs and IPW Estimation” section, and with defined as follows. See Tan (2020b), Section 3.2, for a discussion on how the construction of these estimators is linked to the desired asymptotic expansion (22) for .
The estimator is a regularized weighted least-squares estimator of α1, defined as a minimizer to the penalized loss function
where excluding the intercept , λ ≥ 0 is a tuning parameter, and is the weighted least-squares loss,
That is, the observations in the treated group are weighted by , which differs slightly from the commonly used inverse probability weight . Larger weights are associated with observations with lower-fitted PSs, thereby requiring model (16) to be better fitted in covariate regions with more missing data.
Similarly as discussed regarding , there are simple and interesting implications of the estimator . By the KKT condition for minimizing (18), the fitted OR function satisfies
In (20), the inequality reduces to equality for any j such that the jth estimate is nonzero. Equation (19) implies that the estimator can be recast as
which takes the form of linear prediction estimators known in the survey literature (eg, Sarndal et al. 1992): , for some fitted OR function . As a consequence, always falls within the range of the observed outcomes {Yi: Ti = 1, i = 1,…,n} and the predicted values . This boundedness property is not satisfied by the estimator , where and are the fitted values similar to and in the “Setup” section but based on regularized likelihood estimation in OR and PS models.
We provide a high-dimensional analysis of the proposed estimator , allowing for possible model misspecification. See Tan (2020b, Section 3.3) for a detailed discussion. In contrast, with asymptotic expansion (7) for with correctly specified OR and PS models, our main result shows that under suitable conditions, the estimator admits the asymptotic expansion
where , , and and are limit or target values defined as follows. With possible model misspecification, the target value is defined as a minimizer of the expected calibration loss
If PS model (8) is correctly specified, then . Otherwise, may differ from π*(X). The target value is defined as a minimizer of the expected loss
If OR model (16) is correctly specified, then . But may in general differ from m1*(X). Then, Tan (2020b), Proposition 1, shows that if either logistic PS model (8) or linear OR model (16) is correctly specified, the following results hold under suitable conditions related to the sparsity of the target values and .
- is consistent for μ1 and asymptotically normally distributed:(23)where .
- A consistent estimator of V is(24)
- An asymptotic (1 − c) CI for μ1 is(25)where zc/2 is the (1 − c/2) quantile of N(0,1). Hence, a doubly robust CI for μ1 is obtained.
Next, we present model-assisted CIs for μ1, in the setting where a generalized linear OR model is used together with a logistic PS model. Consider a generalized linear OR model with a canonical link,
that is, model (1) with the vector of covariate functions g1 (X) taken to be the same as f (X) in model (8). Our point estimator of μ1 is as defined in (17), where and . The estimator is the regularized calibrated estimator of γ as before. However, is a regularized weighted likelihood estimator of α1, defined as a minimizer of the penalized loss function
where , excluding the intercept , λ ≥ 0 is a tuning parameter, and is the weighted likelihood loss,
with . The regularized weighted least-squares estimator for a linear OR model is recovered in the special case of the identity link, ψ(u) = u and Ψ(u) = u2/2. In addition, the KKT condition for minimizing the penalized loss function (27) remains the same as in (19) and (20); hence, the estimator can be put in the prediction form (21), which ensures that the boundedness property that always falls within the range of the observed outcomes {Yi: Ti = 1, i = 1,…, n} and the predicted values .
Tan (2020b, Proposition 3) shows that if logistic PS model (8) is correctly specified but OR model (26) may be misspecified, then admits asymptotic expansion (22) with , and results (23) to (25) hold under suitable conditions, where and the target value is defined as a minimizer of the expected loss , similar to before. The CIs obtained for μ1 are said to be PS based, OR assisted. We make the following remarks:
- As mentioned in Tan (2020b, Section 3.4), it is also possible to derive OR-based, PS-assisted CIs for μ1 with a nonlinear OR model. In that case, an estimator of γ would be defined depending on an estimator of α1, similar to how is defined depending on .
- The preceding PS-based, OR-assisted CIs are convenient when ATEs associated with several outcomes need to be estimated using the same set of fitted PSs. Moreover, regularized calibration estimation of PSs enjoys attractive properties, as discussed in the “PSs and IPW Estimation” section.
- With additional complexity, a 2-step procedure was developed by Ghosh and Tan (2020) to obtain doubly robust CIs for μ1.
Our theory and methods are presented mainly on estimation of μ1, but they can be directly extended for estimating μ0 and hence ATE, that is, μ1 − μ0. Consider a logistic PS model (8) and a generalized linear OR model,
where f(X) is the same vector of covariate functions as in PS model (8) and α0 is a vector of unknown parameters. Our point estimator of ATE is , and that of μ0 is
where φ() is defined in (6), , and . The estimator is the same regularized calibrated estimator as in the “PSs and IPW Estimation” section. The estimator is defined similarly as , but with the loss function in (27) replaced by
Under similar conditions as in the estimation of μ1, the estimator admits the asymptotic expansion
where , , and and are the target values defined similarly as and . Then, Wald CIs for μ0 and ATE can be derived similarly as in the estimation of μ0 and shown to be either doubly robust in the case of linear OR models, or valid if PS model (8) is correctly specified but OR models (26) and (28) may be misspecified for nonlinear outcome models.
The proposed method for model-assisted inference about ATEs is implemented as part of the publicly released R package RCAL (Tan & Sun 2020). The package provides both functions for regularized calibrated estimation of PSs and OR functions and for subsequent estimation of ATEs. In addition to a full reference manual, a vignette is also included in the package to give a direct and accessible introduction to the method with simple examples.
To facilitate applications, we focus on the parametric setting as described in the “Setup” section, where OR and PS models are generalized linear regressions in the usual form but prespecified with possibly a large number of regressors. Each regressor is a known function of the covariates, for example, the main effect or a spline term of a single covariate or an interaction of 2 covariates. Our method employs Lasso-type-penalized estimation to perform variable selection (or, more precisely, regressor selection). For technical justification, our theory is developed in Tan (2020a b) with suitable assumptions regarding the exact sparsity (ie, the number of nonzero coefficients) on the limit values of the estimators in OR and PS models, which may be misspecified. Nevertheless, various extensions can be investigated. For example, approximate or weak sparsity can be accommodated, along similar lines as in Negahban et al (2012), Smucler et al (2019), and Bradic et al (2021). Moreover, regularized calibrated estimation can be combined with related methods, such as nonlinear regression models (Hastie et al. 2009), targeted maximum likelihood estimation (van der Laan & Rubin 2006; van der Laan & Rose 2017), and ensemble learning (van der Laan et al. 2007).
Simulation Studies
We conduct extensive simulation studies to evaluate the performances of the proposed methods and compare them with existing methods in both low-dimensional and high-dimensional settings. These studies are reported, in full detail, in Tan (2020a) for PS estimation and in Tan (2020b) for model-assisted inference about ATEs. Below, we describe the simulation study in Tan (2020b, Section 4).
Let X = (X1, …, Xp) be multivariate normal with means 0 and covariances cov (Xj, Xk) = 2−|j−k| for 1 ≤ j, k ≤ p. In addition, let for j = 1,…, 4. Consider the following data-generating configurations:
- C1.
Generate T given X from a Bernoulli distribution with
and, independently, generate Y1 given X from a normal distribution with variance 1 and mean
- C2.
Generate T given X as in (C1), but, independently, generate Y1 given X from a normal distribution with variance 1 and mean
- C3.
Generate Y1 given X as in (C1), but, independently, generate T given X from a Bernoulli distribution with
To study the estimation of μ1, note that the observed data consist of independent and identically distributed observations {(TiYi, Yi, Xi): i = 1,…, n}. Consider logistic PS model (8) and linear OR model (16), both with fj(X) = Xj for j = 1,…, p. Then, the 2 models can be classified as follows, depending on the data configuration above:
- C1.
PS and OR models both correctly specified
- C2.
PS model correctly specified, but OR model misspecified
- C3.
PS model misspecified, but OR model correctly specified
The true OR model in (C2) and PS model in (C3) are nonlinear (in the linear or logistic scale) in the regressors X1,…, Xp used. See the supplemental material in Tan (2020b) for boxplots of Xj within {T = 1} and {T = 0} and scatterplots of Y against Xj within {T = 1} for j = 1,…, 4. Partly because is a monotone function of Xj, the misspecified OR model in (C1) or PS model in (C2) appears to be difficult to detect by standard model diagnosis.
For n = 800 and p = 200 or 1000, Table 1 summarizes the results for estimation of μ1, based on 1000 repeated simulations. The methods RML and RCAL perform similarly to each other in terms of bias, variance, and coverage in the cases (C1) and (C3); however, RCAL leads to noticeably smaller absolute biases and better coverage than RML in (C2), when there are correct PS and misspecified OR models. The post-Lasso refitting method, RML2, yields coverage proportions closer to the nominal probabilities than does RCAL, but consistently and, in (C2), substantially higher variances and wider CIs. These properties can also be confirmed from the QQ plots of the estimates and t-statistics in the supplemental material of Tan (2020b).
Empirical Application
Note: The material in this section is adapted from Tan Z. Regularized calibrated estimation of propensity scores with model misspecification and high-dimensional data. Biometrika. 2020;107;137-158; and Tan Z. Model-assisted inference for treatment effects using regularized calibrated estimation with high-dimensional data. Ann Statist. 2020;48:811-837.
We provide an empirical application of the proposed methods to a medical study in Connors et al (1996) on the effects of right heart catheterization.
The observational study of Connors et al (1996) was of interest at the time when many physicians believed that the procedure led to better patient outcomes, but the benefit had not been demonstrated in any randomized clinical trials. The study included n = 5735 critically ill patients who were admitted to 5 medical centers. For each patient, the data consist of treatment status T, defined as 1 if the procedure was used within 24 hours of admission and 0 otherwise; health outcome Y, defined as survival time up to 30 days; and a list of 75 covariates X specified by medical specialists in critical care. For previous analyses using PSs, logistic regression was employed either with main effects only (Hirano & Imbens 2002; Vermeulen & Vansteelandt 2015) or with interaction terms manually added (Tan 2006a) in the approach of Rosenbaum and Rubin (1984).
To explore dependency beyond the main effects of the covariates, we consider a logistic PS model (8) and a logistic OR model (26) for 30-day survival status 1{Y > 30} as a binary outcome, with the regressor vector f (X) including all main effects and 2-way interactions of X except those with the fractions of nonzero values less than 46 (ie, 0.8% of the sample size 5735). The dimension of f (X) is p = 1855, excluding the constant. All variables in f (X) are standardized with sample means 0 and variances 1.
For estimating PSs, we apply regularized calibrated estimation and regularized maximum likelihood. For each method, the Lasso tuning parameter λ is determined using 5-fold cross-validation based on the corresponding loss function. Possible values of λ are searched in the set , where λ* is the value leading to a 0 solution.
To measure the effect of calibration in the treated sample for a function h(X) using a PS estimate , we use the standardized calibration difference , where and denote the sample mean and variance in the overall sample, respectively (including treated and untreated subjects), and is defined as with Y replaced by h(X). For fj(X) standardized with sample mean 0 and sample variance 1, reduces to . See, for example, Austin and Stuart (2015) for a related statistic for balance checking.
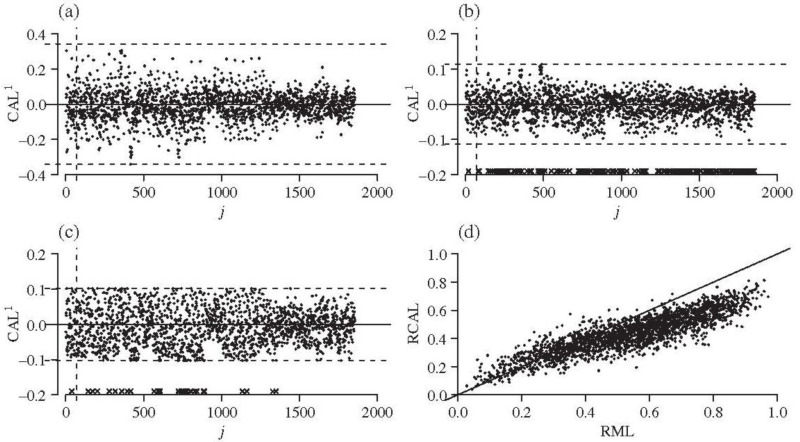
Figure 1 presents the standardized calibration differences for all the variables fj(X) and the fitted PSs in the treated sample. From Table 1, the maximum absolute standardized differences are reduced from 35% to about 10% based on the estimators and . However, the proposed estimator is obtained with a much smaller number, 32 vs 188, of nonzero estimates of coefficients γj in the PS model. The corresponding standardized differences for these 32 nonzero coefficients precisely attain the maximum absolute value, 0.102. The fitted PSs in the treated are consistently larger or smaller than when close to 0 or, respectively, 1. As a result, the inverse probability weights tend to be less variable than , which is also confirmed by Tan (2020a, Figure 5).
Next, we apply the estimators and using regularized calibrated estimation and the corresponding estimators such as using regularized maximum likelihood estimation. A 5-fold cross-validation is also used to select the Lasso tuning parameter for the regularized estimators and . We also compute the (ratio) IPW estimators, such as , along with nominal SEs obtained by ignoring the data dependency of the fitted PSs.
Table 2, reproduced from Tan (2020b), shows various estimates of survival probabilities and ATE. The IPW estimates from RCAL estimation of PSs have noticeably smaller nominal SEs than does RML estimation, for example, with the relative efficiency (0.026/0.023)2 = 1.28 for estimation of μ1. This improvement can also be seen from Figure S7 in the supplemental material of Tan (2020b), where the RCAL inverse probability weights are much less variable than are RML weights.
The augmented IPW estimates and CIs are similar to each other from RCAL and RML estimation. The estimate of μ1 from RML with post-Lasso refitting appears problematic, with a large SE. However, the validity of RML CIs depends on both PS and OR models being correctly specified, whereas that of RCAL CIs holds even when the OR model is misspecified. While an assessment of this difference is difficult with real data, Figure S7 in the supplemental material of Tan (2020b) shows that the sample influence functions for ATE using RCAL estimation appear to be more normally distributed, especially in the tails, than with RML estimation.
Finally, the augmented IPW estimates of the ATE are smaller in absolute values, and also with smaller SEs, than previous estimates based on main-effect models: about −0.060 ± 2 × 0.015 (Vermeulen & Vansteelandt 2015). The reduction in SEs might be explained by the well-known property that an augmented IPW estimator has a smaller asymptotic variance when obtained using a larger (correct) PS model.
Instrumental Variables
Framework
As mentioned in the “Setup” section, one of the assumptions needed to achieve point identification of ATEs is unconfoundedness, that is, all confounding variables related to both treatment status and potential outcomes should be measured and included as covariates in the analysis. IV methods are useful for CER in the presence of unmeasured confounding where some covariates underlying selection bias are unmeasured.
The conventional IV method (eg, Wooldridge 2002) has been widely used in econometrics since the publication of Wright (1928). This method deals with estimation of ATEs for continuous outcomes but implicitly assumes that individual treatment effects are homogeneous, independent of the treatment and instrument given the covariates (Heckman 1997). Recently, while handling continuous or discrete outcomes and allowing heterogeneous treatment effects, a rigorous IV framework was formulated in terms of potential treatment status and potential outcomes (Robins 1994; Angrist et al. 1996).
We describe the IV framework at the population level. Let Z be an instrument, D a treatment (in place of T in the “Propensity Scores and Unconfounded Estimation” section), Y an outcome of interest, and X a vector of preinstrument, pretreatment covariates. For simplicity, assume that both Z and D are dichotomous, taking value 0 or 1. For z ∈ {0, 1} and d ∈ {0, 1}, let Dz be the potential treatment status that would be observed if Z were set to z, and let Yzd be the potential outcome that would be observed if Z were set to z and D were set to d. By consistency, we assume that D = Dz if Z = z, and Y = Yzd if Z = z and D = d. The basic assumptions for a valid IV are as follows:
- IV.1.
Instrumentation: the instrument Z is associated with the treatment D;
- IV.2.
Exclusion restriction: Yzd = Yz′d, denoted as Yd, for z ≠ z′ and d = 0, 1;
- IV.3.
IV unconfoundedness: Z and (Dz, Yzd) are conditionally independent given X for z ∈ {0, 1} and d ∈ {0, 1};
- IV.4.
IV overlap: 0 < π*(X) < 1, where π*(X) = P(Z = 1│X) is called the instrument PS (Tan 2006b).
By the first 2 assumptions, an IV affects treatment status but has no direct effect on potential outcomes. By the last 2 assumptions, an IV serves as an experimental handle similarly as in the unconfoundedness and overlaps assumptions in the “Propensity Scores and Unconfounded Estimation” section. In particular, the instrument is allowed to be associated with the covariates, so that the groups with different instrumental levels (ie, different instrument groups) may differ in their distributions of the covariates. There has been increasing research on how to evaluate and conduct IV analysis in such situations (eg, Brookhart et al. 2007; Baiocchi et al. 2012).
The basic IV assumptions stated above, in general, do not yield point identification of ATEs or ATTs, although bounds can be obtained (Manski 1990; Balke & Pearl 1997). Additional assumptions can be imposed to identify specific treatment parameters. In the case of dichotomous D and Z, each subject can be classified into 1 of the 4 groups, depending on the values of (D0, D1): compliers (D0 = 0 and D1 = 1), always-takers (D0 = D1 = 1), never-takers (D0 = D1 = 0), and defiers (D0 = 1 and D1 = 0). We focus on the approach based on the monotonicity assumption (Angrist et al. 1996):
- IV.5.
Monotonicity: there exists no defier; that is, D0 ≤ D1, in the population.
Under this assumption (in addition to the basic IV assumptions), the local ATE (LATE), also called the complier ATE, is defined as LATE (x) = E(Y1 − Y0 |D0 < D1, X = x) and can be identified by
For high-dimensional covariates X, LATE(x) is difficult to interpret, depending on all covariates. Moreover, estimation of LATE(x) can be sensitive to modeling assumptions on the conditional expectations above. Hence, it is of interest to consider the population LATE (or in short LATE), defined as LATE = E(Y1 − Y0 |D0 < D1). As shown by Tan (2006b) and Frolich (2007), the LATE can be identified in 2 distinct ways:
depending on the regression functions E(Y│Z = z, X) and E(D│Z = z, X) for z ∈ {0, 1}, or
depending on the instrument PS π*(X) = P(Z = 1|X). Both (29) and (30) are in the form of a ratio of the difference in outcome Y over that in treatment D.
A further identification to be exploited in our approach is that the individual expectations θd = E(Yd |D0 < D1) for d ∈ {0, 1}, not just the difference LATE = θ1 − θ0, can also be identified. In fact, θ1 is identified as
or equivalently as
Similarly, θ0 is identified as (31) or (32) with D replaced by 1 − D. The difference of the corresponding identification equations for θ1 and θ0 leads back to (29) or (30). As shown in Tan (2006b), both (31) and (32) can be derived from the following expression of θ1:
which is a ratio of 2 differences, depending on potential outcomes and treatments. Because Z is an experimental handle with (D, Y) as “outcomes” under Assumption (IV.3) (instrument unconfoundedness), each expectation in the numerator and denominator of (33) can be identified through OR averaging or inverse probability weighting, so that (31) or (32) is obtained. These results are parallel to related identification results under the assumption of treatment unconfoundedness (Tan 2007).
Existing Estimators
Suppose that {Oi = (Yi, Di, Zi, Xi): i = 1, …, n} are independent and identically distributed observations of O = (Y, D, Z, X), where Y is an outcome, D is a binary treatment, Z is a binary instrument, and X is a vector of measured covariates. For estimating (θ1, θ0) and LATE from sample data, additional modeling assumptions are required to estimate unknown functions in the identification equations (29) and (30) or (31) and (32). There are at least 2 distinct approaches, depending on models for the instrument PS π*(x) = P(Z = 1│X = x) or treatment and OR functions and for d, z ∈ {0, 1} (Tan 2006b). For simplicity, estimation of θ1 is discussed, whereas that of θ0 can be similarly handled. Throughout, denotes a sample average such that for a function b(O).
First, consider an instrument PS model,
where Π(∙) is an inverse link function, f(x) = {1, f1(x),…,fp(x)}T is a vector of known functions, and γ = (γ0, γ1,…, γp)T is a vector of unknown parameters. For concreteness, assume that logistic regression is used such that π(x; y) = [1 + exp{−γTf(x)}]−1. By (32), the IPW estimator of θ1 is
where is a fitted instrument PS. For low-dimensional X, is customarily the maximum likelihood estimator of γ. In high-dimensional settings, can be a Lasso-penalized maximum likelihood estimator .
Alternatively, for z ∈ {0, 1}, consider treatment and OR models, which can both be called “outcome regression” with (D, Y) as “outcomes”:
where ψD(∙) and ψY(∙) are inverse link functions, and are 2 vectors of known functions, and αz and α1z are 2 vectors of unknown parameters of dimensions 1 + q1 and 1 + q2 respectively. By (31), the OR-based estimator of θ1 is
where , , and, for z ∊ {0,1}, is a fitted treatment regression function and is a fitted OR function. For low-dimensional X, and are customarily maximum quasi-likelihood estimators of αz and α1z or their variants. In high-dimensional settings, and can be Lasso-penalized quasi-likelihood estimators, and .
The consistency of the estimator relies on correct specification of model (34), whereas the consistency of relies on correct specification of models (35) and (36). The weighting and regression approaches can be combined to obtain doubly robust estimators through augmented IPW estimation (Tan 2006b), in a similar manner as in the setting of treatment unconfoundedness (Robins et al. 1994; Tan 2007). The expectations E(D1) and E(D0) in (33) can be estimated by and , respectively, where
Similarly, the expectations E(D1 Y1) and E(D0 Y1) in (33) can be estimated by and respectively, where
By (33), the resulting doubly robust estimator of θ1 is
where and . Consistency of can be achieved if either model (34) or models (35) and (36) are correctly specified.
There is potentially another advantage of doubly robust estimators in high-dimensional settings. In this case, the estimator or in general converges at a lower rate than does to the true value θ1 under correctly specified model (34) or models (35) and (36), respectively. Denote , , and , obtained from Lasso-penalized likelihood estimation. By related results in Chernozhukov et al (2018, Section 5.2), it can be shown that if all models (34) and (35) and (36) are correctly specified, under suitable sparsity conditions, the estimator converges to θ1 at rate and admits the asymptotic expansion
where π*(X) = π(X; γ*), , and , with the true values in models (34), (35), and (36). From this expansion, valid Wald CIs based on can be obtained for θ1.
Model-Assisted Inference
We develop new methods and theory using IVs in high-dimensional settings to obtain model-assisted CIs for LATEs, which are valid if the instrument PS model is correctly specified, but the treatment and OR models may be misspecified. The material in this section is based on Sun and Tan (2020).
To focus on main ideas, we describe our new method for estimating θ1. Estimation of θ0 and LATE is discussed later in this section. Similarly as in the “Existing Estimators” section, consider logistic regression model (34) for estimating the instrument PS π*(x) = P(Z = 1|X = x), and models (35) and (36) for estimating treatment and OR functions and , respectively, for z ∈ {0, 1}. For technical reasons, we require that the “regressor” vector f(x) in model (34) is a subvector of g(x) and h(x) in models (35) and (36). This condition can be satisfied possibly after enlarging models (35) and (36) to accommodate f(x).
A class of doubly robust estimators of θ1 slightly more flexible than (41) is
where , with and 2 possibly different versions of fitted values for π*, and with fitted values for respectively, for z ∈ {0, 1}, and with and defined as (37) to (40),
Our point estimator of θ1 is , where, for z ∈ {0, 1}, , , and are fitted values, and are estimators of (γ, αz, α1z) defined as follows.
For logistic regression model (34), the estimator is a regularized calibrated estimator of γ (Tan 2020a), defined as a minimizer of the Lasso-penalized objective function
with the calibration loss functions
For treatment regression model (35), is a regularized weighted likelihood estimator of αz, defined as a minimizer of the Lasso-penalized objective function
with the weighted (quasi-)likelihood loss function
where the weight function is wz(X; γ) = π(X; γ)/{1 − σ(X; γ)} or {1 − π(X; γ)}/π(X; γ) for z = 0 or 1, respectively, and . For OR model (36), is a regularized calibrated estimator of α1z, defined as a minimizer of the Lasso-penalized objective function
with the loss function
where the weight function wz (X; γ) is the same as above, and .
Compared with regularized likelihood estimation in the “Existing Estimators” section, our method involves using a different set of estimators , which are called regularized calibrated estimators. Similarly as in Tan (2020b), these estimators are derived to allow model-assisted, asymptotic CIs for θ1 based on . Before discussing inference properties, we point out several interesting properties algebraically associated with our estimators.
First, by the KKT condition for minimizing (44), the fitted instrument PS satisfies, similarly as in (14) and (15),
These equations also hold with Zi replaced by 1 − Zi and replaced by . Equation (47) shows that the IPWs, with Zi = 1, sum to the sample size n, whereas equation (48) implies that the weighted average of each covariate fj(Xi) over the instrument group {Zi = 1} may differ from the overall average of fj(Xi) by no more than λ. Such differences are of interest in showing how a weighted instrument group resembles the overall sample. In contrast, similar results are not available when using the regularized likelihood estimator .
By the KKT condition associated with the intercept in α1 for minimizing (45), the fitted treatment regression function satisfies, similarly as in (19),
A similar equation holds with Zi replaced by 1 − Zi and replaced by , and by . As a result of (49), our augmented IPW estimator for E(D1), defined as , can be simplified to
Hence, always falls within the range of the binary treatment values {Di: Zi = 1, i = 1,…,n} and the predicted values , which are by definition in the interval [0,1]. This boundedness property is not satisfied by the usual estimator but is desirable for stabilizing the behavior of augmented IPW estimators, especially when used in the denominator of (43).
By the KKT condition associated with the intercept in α1 for minimizing (46), the fitted functions and jointly satisfy
A similar equation holds with Zi replaced by 1 − Zi, replaced by , and replaced by . By (49), our augmented IPW estimator for E(D1 Y1), defined as , can be simplified to
where . As a consequence, always falls within the range of the observed values {DiYi: Zi = 1, i = 1,…,n} and the predicted values .
We provide a high-dimensional analysis of the proposed estimator , provided that instrument PS model (34) is correctly specified but treatment and outcome models (35) and (36) may be misspecified. See Sun and Tan (2020, Section 3) for a detailed discussion. In contrast with the asymptotic expansion (42) for with all correctly specified models (34), (35), and (36), our main result shows that under suitable conditions, is consistent for θ1 and admits the asymptotic expansion
where , , , and, for z ∈ {0,1}, and with the target values defined as the minimizers of the expected loss functions for . Then, Sun and Tan (2020, Proposition 1) show that if instrument PS model (34) is correctly specified but treatment and outcome models (35) and (36) may be misspecified, the following results hold under suitable sparsity conditions.
- is consistent for θ1 and asymptotically normally distributed:where .
- A consistent estimator of V1 iswhere .
- An asymptotic (1 − c) CI for θ1 is
where z(c/2) is the (1 − c/2) quantile of N(0,1).
Next, we describe how our method can be applied to estimate θ0 and LATE, denoted as θ = θ1 − θ0. In addition to models (34), (35), and (36), consider the following OR model in the untreated population for z ∈ {0,1},
where is a vector of known functions, and α0z is a vector of unknown parameters of dimension 1 + q2. For augmented IPW estimation of E{(1 − D0)Y0} and E{(1 − D1)Y1}, define
where is a fitted regression function. Then, a doubly robust estimator of θ0, similar to that of θ1 in (43) is
where , is as in (43), and
Our point estimator of θ0 is and that of LATE, θ = θ1 − θ0, is , where and remain the same as before, and , with defined as follows: for z ∈ {0,1}, let be a minimizer of the Lasso-penalized objective function
with the loss function
where the weight function wz(X; γ) is the same as above. Under similar conditions as in the estimation of θ1, the estimator admits an asymptotic expansion in the form of (51) and Wald CIs for θ0, and LATE can be derived accordingly. In particular, an asymptotic (1 − c) CI for LATE is , where
where .
The proposed method for model-assisted inference using regularized calibrated estimation about LATEs is implemented as part of the publicly released R package RCAL (Tan & Sun 2020). In addition to a full reference manual, a vignette is also included in the package to give a direct and accessible introduction to the method.
Our work focuses on statistical methods and theory for estimation of LATEs in the modern IV framework as described in the “Framework” section. In practice, IV analysis needs to be conducted with care. First, it is often challenging to find valid IVs which can be justified to satisfy the IV assumptions IV.1 to IV.5. Moreover, the IV estimates of treatment effects may suffer large biases or SEs because of possible violations of the IV assumptions or weakness of the IVs in the association with the treatment. There has been extensive research which investigates the impact of weak IVs and related issues in the conventional IV method (Bound et al. 1995; Staiger & Stock 1997; Crown et al. 2011; Andrews et al. 2019), where 2 structural equations are postulated in relating the outcome to the treatment and covariates and then the treatment to the IVs and covariates (Wooldridge 2002). Further work is desired to study how the proposed methods are affected by weak IVs and possible violations of IV assumptions.
Simulation Studies
We present simulation studies to compare pointwise properties of based on regularized likelihood estimation without or with post-Lasso refitting and based on regularized calibrated estimation and coverage properties of the associated CIs. The material in this section is based on Sun and Tan (2020, Section 4).
Let X = (X1,…,Xp) be independent variables where each Xj is N(0,1) truncated to the interval (−2.5,2.5) and then standardized to have mean 0 and variance 1. Consider the transformed variables W1 = exp(0.5 X1), W2 = 10 + {1 + exp(X1)}−1 X2, W3 = (0.04 X1 X3 + 0.6)3, and W4 = (X2 + X4 + 20)2. Let , where is the standardized version of Wj to have mean 0 and variance 1 for j = 1,…,4, and for 5 ≤ j ≤ p. This setup follows that in the preprint Tan (2018) and ensures strict one-to-one mapping between X and X†. See the supplemental material in Sun and Tan (2020) for scatterplots from a simulated data sample of the variables , which are correlated with each other as would be found in real data. Consider the following data-generating configurations:
- C1.
Generate Z given X from a Bernoulli distribution with
Then, independently, generate U from a standard logistic distribution,
and Y1 given X from a normal distribution with variance 1 and mean
- C2.
Generate (Z, U) as in (C1), but generate
and generate Y1 given X from a normal distribution with variance 1 and mean
- C3.
Generate Z given X from a Bernoulli distribution with
and then generate (U, D, Y1) as in (C1).
The observed data consist of independent and identically distributed copies {(YiDi, Di, Zi, Xi): i = 1,…,n}. Consider the following model specifications:
- M1)
logistic instrument PS model (34), logistic treatment model (35), and linear outcome model (36) with for j = 1,…,p.
- M2)
Logistic instrument PS model (34) and logistic treatment model (35) with for j = 1,…,p, and linear outcome model (36) with for j = 1,…,p, 8 additional functions , 4 of which are linear spline basis functions of the fitted values , and 4 are linear spline basis functions of , where the knots are quantiles of the fitted values.
The instrument PS model is correct in configurations (C1) and (C2) but misspecified in configuration (C3). The treatment regression model is correct in configurations (C1) and (C3) but misspecified in (C2), whereas the OR model in either (M1) or (M2) is misspecified in all configurations (C1) to (C3), but it can be regarded as being “closer” to the truth in (C1) and (C3) than in (C2) due to using X† instead of X as regressors. Therefore, the models in both (M1) and (M2) can be classified as follows in configurations (C1) to (C3):
- C1)
Instrument PS model was correctly specified, treatment and OR models were “more correctly” specified;
- C2)
Instrument PS model was correctly specified, treatment and OR models were “less correctly” specified; and
- C3)
Instrument PS model was misspecified, treatment and outcome models were “more correctly” specified.
Similarly as in Kang and Schafer (2007), for p = 4, the treatment and OR models in case (C2) and the instrument PS model in (C3) appear to be adequate by standard diagnosis techniques. See the supplemental material in Sun and Tan (2020) for scatterplots of Y against within {D = 1}, boxplots of within {D = 0} and {D = 1} as well as boxplots of within {Z = 0} and {Z = 1} for j = 1,…,4.
For n = 800 and p = 400 or 1000, Table 3, reproduced from Sun and Tan (2020), summarizes the results based on 1000 repeated simulations. The methods RCAL and RML perform similarly to each other in terms of absolute bias, variance, and coverage in (C1) and (C3), but RCAL yields noticeably smaller absolute biases and better coverage than do RML and RML2 in (C2). The post-Lasso refitting method RML2 appears to achieve coverages closer to the nominal probabilities in (C1) but yields substantially higher variances in all 3 cases (C1) to (C3). These properties can also be seen from the QQ plots of the estimates and t-statistics the supplemental material of Sun and Tan (2020). The performances of each of the 3 methods are similar with models (M1) or (M2) specified. Hence, in the settings studied, there is little benefit in adding the spline terms in the OR model.
Empirical Application
The causal relationship between education and earnings has been of considerable interest in economics. Card (1995) proposed proximity to college as an instrument for completed education. The argument is that proximity to college could be taken as being randomized conditionally on observed covariates, and its influence on earnings could be only through that on the schooling decision. Consider the analytic sample in Card (1995) from the National Longitudinal Survey of Young men, which comprises 3010 men with valid education and wage responses in the 1976 interview. Similarly, as in Tan (2006b), we define the treatment as education after high school, that is, D = 1{years of schooling > 12}; the instrument Z is a binary indicator for proximity to a 4-year college; and the outcome Y is a surrogate outcome constructed for the log of hourly earnings at age 30 years. The raw vector of covariates X include a race indicator; indicators for 9 regions of residence and for residence in SMSA in 1966; mother's and father's years of schooling (momed and daded, respectively); indicators for missing values; indicators for living with both natural parents, with 1 natural parent and 1 stepparent, and with mother only at age 14 years; and the Knowledge of World of Work (kww) score in 1966 and a missing indicator. We use mean imputation for the missing values and standardize all continuous variables with sample mean 0 and variance 1.
We reanalyze the National Longitudinal Survey data to estimate the LATE of education beyond high school on log hourly earnings, using more-flexible, higher-dimensional models than previously allowed. We apply based on regularized calibrated (RCAL) estimation and based on regularized likelihood estimation (RML), as well as the post-Lasso variant (RML2). The specification for f(X) = g(X) consists of all the indicator variables mentioned above, momed, daded, linear spline bases in kww, as well as interactions between the spline terms with all the indicator variables. The vector h(X) augments f(X) and g(X) by adding linear spline terms for each fitted treatment regression , z ∈ {0,1}. We vary the model complexity by considering the number of knots in the set k ∈ {3,9,15}, with knots at the i/(k+1)-th quantiles for i = 1,…,k. The tuning parameter λ is determined using 5-fold cross-validation based on the corresponding penalized loss functions. As an anchor specification, we also consider main-effect models with f(X) = g(X) = (1,XT)T and , where the nuisance parameters are estimated using nonpenalized likelihood or calibration estimation.
Table 4 reproduced from Sun and Tan (2020), shows the estimates of (θ0, θ1) and LATE of education beyond high school on log hourly earnings. Regularized estimation from RCAL, RML, and RML2 yields similar point estimates; the differences are small compared with the SEs. The RCAL and RML estimates have noticeably smaller SEs than do RML2 estimates. Interestingly, for splines with 15 knots, the LATE is estimated from RCAL with a 95% CI of 0.504 ± 0.498, which excludes 0, whereas those from RML and RML2 include 0.
While the validity of CIs is difficult to assess using real data, Figure S9 in the supplemental material of Sun and Tan (2020) shows that the standardized sample influence functions for estimation of LATE. The curves from RCAL appear to be more normally distributed than are those from RML or RML2, especially in the tails. In addition, Figures S10 to S12 in the supplemental material of Sun and Tan (2020) present the standardized calibration differences for all the variables fj(X), j = 1,…,p, similarly to Tan (2020a). Compared with RML and RML2, our method RCAL consistently yields smaller maximum absolute standardized differences and involves fewer nonzero estimates of γj in the instrument PS models.
Conclusions
We developed new statistical methods and theory for tackling 2 broad problems in CER. One is to estimate ATEs using PSs and doubly robust estimators under unconfoundedness. The other is to estimate LATEs using IVs in the presence of possible unmeasured confounding. By these methods, PS and regression models can be fitted with a possibly large number of regressors including main effects and interactions of the covariates, and CIs and hypothesis tests can be obtained about treatment effects in a numerically tractable and statistically principled manner. Our methods are implemented in the publicly released R package RCAL.
There are various interesting topics which warrant further investigation. For the current development, both the instrument and treatment are assumed to be binary. It is desirable to extend our methods to handle multivalued treatments and instruments. Moreover, while the current methods are concerned with causal inference in cross-sectional studies, medical studies frequently involve longitudinal and survival outcomes subject to censoring or dropout. It is also important to extend our methods to handle longitudinal and survival data.
References
- Andrews, I., Stock, J.H., and Sun, L. (2019) “Weak instruments in instrumental variables regression: Theory and Practice,” Annual Review of Economics, 11, 727-53.
- Angrist, J.D., Imbens, G.W., and Rubin, D.B. (1996) “Identification of causal effects using instrumental variables” (with discussion) , Journal of the American Statistical Association, 91, 444-472.
- Austin, P.C. and Stuart, E.A. (2015) “Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies,” Statistics in Medicine, 34, 3661-3679. [PMC free article: PMC4626409] [PubMed: 26238958]
- Balke, A., and Pearl, J. (1997) “Bounds on treatment effects from studies with imperfect compliance,” Journal of the American Statistical Association, 92, 1171-1176.
- Baiocchi, M., Small, D.S., Yang, L., Polsky, D., and Groeneveld, P.W. (2012) “Near/far matching: a study design approach to instrumental variables,” Health Services and Outcomes Research Methodology, 12, 237-253. [PMC free article: PMC4831129] [PubMed: 27087781]
- Belloni, A., Chernozhukov, V., and Hansen, C. (2014) “Inference on treatment effects after selection among high-dimensional controls,” Review of Economic Studies, 81, 608--650.
- Bohning, D. and Lindsay, B.G. (1988) “Monotonicity of quadratic approximation algorithms,” Annals of the Institute of Statistical Mathematics, 40, 641-663.
- Bound, J., Jaeger, D.A., and Bakar, R.M. (1995) “Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak,” Journal of the American Statistical Association, 90, 443-50.
- Bradic, J., Chernozhukov, V., Newey, W. K., and Zhu, Y. (2021) “Minimax semiparametric learning with approximate sparsity,” arXiv:1912.12213v3.
- Brookhart, M.A., Rassen, J.A., Wang, P.S., Dormuth, C., Mogun, H., and Schneeweiss, S. (2007) “Evaluating the validity of an instrumental variable study of neuroleptics,” Medical Care, 45, S116-S122. [PubMed: 17909369]
- Buhlmann, P. and Hothorn, T. (2007) “Boosting algorithms: regularization, prediction and model fitting” (with discussion), Statistical Science, 22, 477-505.
- Buhlmann, P. and van de Geer, S. (2011) Statistics for High-Dimensional Data: Methods, Theory and Applications, Springer.
- Card, D. (1995) “Using Geographic Variation in College Proximity to Estimate the Return to Schooling,” in Aspects of Labor Market Behavior: Essays in Honor of John Vanderkamp, eds. L. N. Christophides, E. K. Grant, and R. Swidinsky. University of Toronto Press, pp. 201-222.
- Chan, K.C.G., Yam, S.C.P., and Zhang, Z. (2016) “Globally efficient non-parametric inference of average treatment effects by empirical balancing calibration weighting,” Journal of the Royal Statistical Society, Ser. B, 78, 673-700. [PMC free article: PMC4915747] [PubMed: 27346982]
- Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C., Newey, W. and Robins, J.M. (2018) “Double/debiased machine learning for treatment and structural parameters,” The Econometrics Journal, 21, C1-C68.
- Connors, A. F., Speroff, T., Dawson, N. V., et al. (1996) “The Effectiveness of Right Heart Catheterization in the Initial Care of Critically Ill Patients,” Journal of the American Medical Association, 276, 889-897. [PubMed: 8782638]
- Crown, W.H., Henk, H.J., and Vanness, D.J. (2011) “Some cautions on the use of instrumental variables estimators in outcomes research: How bias in instrumental variables estimators is affected by instrument strength, instrument contamination, and sample size,” Value in Health, 14, 1078-1084. [PubMed: 22152177]
- Dukes, O. and Vansteelandt, S. (2021) “Inference for treatment effect parameters in potentially misspecified high-dimensional models,” Biometrika, 2, 321-334.
- Farrell, M.H. (2015) “Robust inference on average treatment effects with possibly more covariates than observations,” Journal of Econometrics, 189, 1-23.
- Folsom, R.E. (1991) “Exponential and logistic weight adjustments for sampling and nonresponse error reduction,” Proceedings of the American Statistical Association, Social Statistics Section, 197-202.
- Friedman, J., Hastie, T., and Tibshirani, R. (2000) “Additive logistic regression: A statistical view of boosting” (with discussion), Annals of Statistics, 28, 337-407.
- Friedman, J., Hastie, T. and Tibshirani, R. (2010) “Regularization paths for generalized linear models via coordinate descent,” Journal of Statistical Software, 33, 1-22. [PMC free article: PMC2929880] [PubMed: 20808728]
- Frolich, M. (2007) “Nonparametric IV estimation of local average treatment effects with covariates,” Journal of Econometrics, 139, 35-75.
- Gerhard, T., Huybrechts, K., Olfson, M., et al. (2014) “Comparative mortality risks of antipsychotic medications in community dwelling older adults,” British Journal of Psychiatry, 205, 44-51. [PubMed: 23929443]
- Ghosh, S. and Tan, Z. (2020) “Doubly robust semiparametric inference using regularized calibrated estimation with high-dimensional data,” arXiv:2009.12033.
- Graham, B.S., de Xavier Pinto, C.C., and Egel, D. (2012) “Inverse probability tilting for moment condition models with missing data,” Review of Economic Studies, 79, 1053-1079.
- Hainmueller, J. (2012) “Entropy balancing for causal effects: Multivariate reweighting method to produce balanced samples in observational studies, Political Analysis, 20, 25-46.
- Hastie, T., Tibshirani, R., and Friedman, J. (2009) The Elements of Statistical Learning (2nd edition), Springer.
- Hastie, T., Tibshirani, R., and Wainwright, M. (2015) Statistical Learning with Sparsity: The Lasso and Generalizations, Chapman & Hall.
- Heckman, J.J. (1997) “Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations,” Journal of Human Resources, 32, 441-462.
- Hernan, M.A. and Robins, J. M. (2006) “Instruments for causal inference: An epidemiologist's dream?” Epidemiology, 360-372. [PubMed: 16755261]
- Hirano, K., and Imbens, G.W. (2002) “Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization,” Health Services and Outcomes Research Methodology, 2, 259-278.
- Hirshberg, D.A. and S. Wager (2021) “Augmented Minimax Linear Estimation,” Annals of Statistics, to appear.
- Holland, P.W. (1986) “Statistics and causal inference” (with discussion), Journal of the American Statistical Association, 81, 945-970.
- Huybrechts, K., Gerhard, T., Franklin, J.M., Levin, R., Crystal, S., and Schneeweiss, S. (2014) “Instrumental variable applications using nursing home prescribing preferences in comparative effectiveness research,” Pharmacoepidemiology and Drug Safety, 23, 830-838. [PMC free article: PMC4116440] [PubMed: 24664805]
- Imai, K. and Ratkovic, M. (2014) “Covariate balancing propensity score,” Journal of the Royal Statistical Society, Ser. B, 76, 243-263.
- Javanmard, A. and Montanari, A. (2014) “Confidence intervals and hypothesis testing for high-dimensional regression,” Journal of Machine Learning Research, 15, 2869-2909.
- Kang, J.D.Y. and Schafer, J.L. (2007) “Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data” (with discussion), Statistical Science, 523-539. [PMC free article: PMC2397555] [PubMed: 18516239]
- Kim, J.K. and Haziza, D. (2014) “Doubly robust inference with missing data in survey sampling,” Statistica Sinica, 24, 375-394.
- Lee, B.K., Lessler, J., Stuart, E.A. (2010) “Improving propensity score weighting using machine learning,” Statistics in Medicine, 29, 337-346. [PMC free article: PMC2807890] [PubMed: 19960510]
- Manski, C.F. (1990) “Nonparametric bounds on treatment effects,” American Economic Review, 80, 319-323.
- McCaffrey, D.F., Ridgeway, G., and Morral, A.R. (2004) “Propensity score estimation with boosted regression for evaluating causal effects in observational studies,” Psychological Methods, 9, 403-425. [PubMed: 15598095]
- McCullagh, P. and Nelder, J. (1989) Generalized Linear Models (2nd edition), Chapman & Hall.
- Morgan, S.L. and Winship, C. (2014) Counterfactuals and Causal Inference: Methods and Principles for Social Research (second ed.), Cambridge University Press.
- Neyman, J. (1923) “On the application of probability theory to agricultural experiments: Essay on principles, Section 9,” translated in Statistical Science, 1990, 5, 465-480.
- Ning, Y., Peng, S., and Imai, K. (2020) “Robust estimation of causal effects via a high-dimensional covariate balancing propensity score,” Biometrika, 107, 533-554.
- Osborne, M., Presnell, B., and Turlach, B. (2000) “A new approach to variable selection in least squares problems,” IMA Journal of Numerical Analysis, 20, 389-404.
- Patient-Centered Outcomes Research Institute (PCORI) Methodology Committee (2021) The PCORI Methodology Report. PCORI.
- Robins, J.M. (1994) “Correcting for non-compliance in randomized trials using structural nested mean models,” Communications in Statistics, 23, 2379-2412.
- Robins, J.M., Rotnitzky, A., and Zhao, L.P. (1994) “Estimation of regression coefficients when some regressors are not always observed,” Journal of the American Statistical Association, 89, 846-866.
- Robins, J.M., Li, L., Mukherjee, R., Tchetgen, E.T., and van der Vaart, A. (2017) “Minimax estimation of a functional on a structured high-dimensional model,” Annals of Statistics, 45, 1951-1987. [PMC free article: PMC6453538] [PubMed: 30971851]
- Rosenbaum, P.R. and Rubin, D.B. (1983) “The central role of the propensity score in observational studies for causal effects,” Biometrika, 70, 41-55.
- Rosenbaum, P.R. and Rubin, D.B. (1984) “Reducing bias in observational studies using subclassification on the propensity score,” Journal of the American Statistical Association, 79, 516-524.
- Rubin, D.B. (1974) “Estimating causal effects of treatments in randomized and nonrandomized Studies,” Journal of Educational Psychology, 66, 688-701.
- Rubin, D.B. (1976) Inference and missing data, Biometrika, 63, 581-590.
- Sarndal, C.E., Swensson, B. and Wretman, J.H. (1992) Model Assisted Survey Sampling, Springer.
- Schapire, R.E. and Freund, Y. (2012) Boosting: Foundations and Algorithms, MIT Press.
- Setoguchi, S., Schneeweiss, S., Brookhart, M.A., Glynn, R.J., and Cook, E.F. (2008) “Evaluating uses of data mining techniques in propensity score estimation: a simulation study,” Pharmacoepidemiology and Drug Safety, 17, 546-555. [PMC free article: PMC2905676] [PubMed: 18311848]
- Smucler, E., Rotnitzky, A., and Robins, J. M. (2019) “A unifying approach for doubly robust ℓ1 regularized estimation of causal contrasts,” arXiv:1904.03737.
- Staiger D. and Stock J.H. (1997) “Instrumental variables regression with weak instruments,” Econometrica, 65, 557-86.
- Stroup, T.S., Gerhard, T., Crystal, S., Huang, C., Tan, Z., Wall, M.M., Mathai, C., Olfson, M. (2019) Comparative effectiveness of adjunctive psychotropic medications in patients with schizophrenia, JAMA Psychiatry, 76, 508-515. [PMC free article: PMC6495353] [PubMed: 30785609]
- Sun, B. and Tan, Z. (2020) “High-dimensional model-assisted inference for local average treatment effects with instrumental variables,” arXiv:2009.09286.
- Tan, Z. (2006a) “A distributional approach for causal inference using propensity scores,” Journal of the American Statistical Association, 101, 1619-1637.
- Tan, Z. (2006b) “Regression and weighting methods for causal inference using instrumental variables,” Journal of the American Statistical Association, 101, 1607-1618.
- Tan, Z. (2007) “Comment: Understanding OR, PS and DR,” Statistical Science, 22, 560-568.
- Tan, Z. (2010a) “Bounded, efficient, and doubly robust estimation with inverse weighting,” Biometrika, 97, 661-682.
- Tan, Z. (2010b) “Marginal and nested structural models using instrumental variables,” Journal of the American Statistical Association, 105, 157-169.
- Tan, Z. (2010c) “Nonparametric likelihood and doubly robust estimating equations for marginal and nested structural models,” Canadian Journal of Statistics, 38, 609-632.
- Tan, Z. (2018) “Model-assisted inference for treatment effects using regularized calibrated estimation with high-dimensional data,” arXiv:1801.09817.
- Tan, Z. (2020a) “Regularized calibrated estimation of propensity scores with model misspecification and high-dimensional data,” Biometrika, 107, 137-158.
- Tan, Z. (2020b) “Model-assisted inference for treatment effects using regularized calibrated estimation with high-dimensional data,” Annals of Statistics, 48, 811-837.
- Tan, Z. and Sun, B. (2020) RCAL: Regularized calibrated estimation, R package version 2.0, available at https://cran
.r-project .org/web/packages/RCAL/index.html - Tibshirani, R. (1996) “Regression shrinkage and selection via the Lasso” Journal of the Royal Statistical Society, Ser. B, 58, 267-288.
- Tsiatis, A.A. (2006) Semiparametric Theory and Missing Data, Springer.
- van der Laan, M.J., Benkeser, D., and Cai, W. (2019) “Efficient estimation of pathwise differentiable target parameters with the undersmoothed highly adaptive Lasso,” arXiv:1908.05607. [PMC free article: PMC10238856] [PubMed: 35851449]
- van der Laan, M.J., Polley, E.C., and Hubbard, A.E. (2007) “Super learning,” Statistical Applications in Genetics and Molecular Biology, 6, Article 25. [PMC free article: PMC2473869] [PubMed: 17402922]
- van der Laan, M.J. and Robins, J.M. (2003) Unified Methods for Censored Longitudinal Data and Causality, Springer.
- van der Laan, M.J. and Rose, S. (2017) Targeted Learning in Data Science: Causal Inference for Complex Longitudinal Studies, Springer.
- van der Laan, M.J. and Rubin, D.B. (2006) “Targeted maximum likelihood learning,” International Journal of Biostatistics, 2, Article 11. van de Geer, S., Buhlmann, P., Ritov, Y., Dezeure, R. (2014) “On asymptotically optimal confidence regions and tests for high-dimensional models,” Annals of Statistics, 42, 1166-1202.
- Vermeulen K. and Vansteelandt, S. (2015) “Bias-reduced doubly robust estimation,” Journal of the American Statistical Association, 110, 1024-1036.
- Weitzen, S., Lapane, K.L., Toledano, A.Y., Hume, A.L., Mor, V. (2004) “Principles for modeling propensity scores in medical research: a systematic literature review,” Pharmacoepidemiology and Drug Safety, 13, 841-853. [PubMed: 15386709]
- Westreich, D., Cole, S.R., Funk, M.J., Brookhart, M.A., and Stürmer, T. (2011) “The role of the c-statistic in variable selection for propensity score models,” Pharmacoepidemiology and Drug Safety, 20, 317-320. [PMC free article: PMC3081361] [PubMed: 21351315]
- Winterstein, A.G., Gerhard, T., Kubilis, P., Linden, S., Shuster, J., Zito, J., Crystal, S., and Olfson, M. (2012) “Cardiovascular safety of central nervous system stimulants in children and adolescents,” BMJ, 345, e4627. [PMC free article: PMC3399772] [PubMed: 22809800]
- Wooldridge, J.M. (2002) Econometric Analysis of Cross Section and Panel Data, MIT Press.
- Wright, S. (1928) The Tariff on Animal and Vegetable Oils, MacMillan, the Appendix.
- Wu, T.T. and Lange, K. (2010) “The MM alternative to EM,” Statistical Science, 25, 492-505.
- Wyss, R., Ellis, A.R., Brookhart, M.A., Girman, C.J., Funk, M.J., LoCasale, R., and Stürmer, T. (2014) “The role of prediction modeling in propensity score estimation: An evaluation of logistic regression, bCART, and the covariate-balancing propensity score,” American Journal of Epidemiology, 645-655. [PMC free article: PMC4157700] [PubMed: 25143475]
- Yang, T. and Tan, Z. (2018) “Backfitting algorithms for total-variation and empirical-norm penalized additive modeling with high-dimensional data,” Stat, 7, e198.
- Zhang, C.-H. and Zhang, S.S. (2014) “Confidence intervals for low-dimensional parameters with high-dimensional data,” Journal of the Royal Statistical Society, Ser. B, 76, 217-242.
Related Publications
- Ghosh S, Tan Z. Doubly robust semiparametric inference using regularized calibrated estimation with high-dimensional data. 2020. Accessed November 30, 2021. arXiv:2009.12033
- Sun B, Tan Z. High-dimensional model-assisted inference for local average treatment effects with instrumental variables. 2020. Accessed November 30, 2021. arXiv:2009.09286
- Tan Z. Analysis of odds, probability, and hazard ratios: From 2 by 2 tables to two-sample survival data. 2019. Accessed November 30, 2021. arXiv:1911.10682
- Tan Z, Zhang C.-H. Doubly penalized estimation in additive regression with high-dimensional data. Ann Statist. 2019;47:2567-2600.
- Tan Z. Regularized calibrated estimation of propensity scores with model misspecification and high-dimensional data. Biometrika. 2020;107:137-158.
- Tan Z. Model-assisted inference for treatment effects using regularized calibrated estimation with high-dimensional data. Ann Statist. 2020;48:811-837.
Acknowledgment
Research reported in this report was funded through a Patient-Centered Outcomes Research Institute® (PCORI®) Award (ME-1511-32740). Further information available at: https://www.pcori.org/research-results/2016/developing-new-methods-causal-inference-observational-studies
Figures
Figure 1Standardized Calibration Differences Plotted Against Index j for the Estimators (a) , (b) , and (c) With λ Selected by Cross-Validationa
aIn each panel, a vertical line is placed at the end of the indices for 71 main effects, and 2 horizontal lines are placed at the maximum absolute standardized differences; crosses (x) mark the indices j corresponding to 188 nonzero estimates of γj for and 32 nonzero estimates of γj for . (d) Fitted PSs (Xi), (Xi) in the treated sample {i: Ti = 1, i = 1,…, n}.
Tables
Table 1Summary of Results With Linear Outcome Modelsa
| (C1) cor PS, cor OR | (C2) cor PS, mis OR | (C3) mis PS, cor OR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RML | RML2 | RCAL | RML | RML2 | RCAL | RML | RML2 | RCAL | |
| n = 800 and p = 200 | |||||||||
| Bias | 0.019 | 0.002 | 0.026 | −0.038 | −0.009 | 0.012 | 0.010 | 0.002 | 0.016 |
| 0.070 | 0.079 | 0.070 | 0.072 | 0.092 | 0.071 | 0.070 | 0.076 | 0.070 | |
| 0.068 | 0.076 | 0.068 | 0.072 | 0.094 | 0.069 | 0.069 | 0.075 | 0.068 | |
| Cov90 | 0.864 | 0.880 | 0.854 | 0.859 | 0.906 | 0.889 | 0.875 | 0.886 | 0.871 |
| Cov95 | 0.922 | 0.947 | 0.914 | 0.914 | 0.950 | 0.938 | 0.941 | 0.950 | 0.942 |
| n = 800 and p = 1000 | |||||||||
| Bias | 0.031 | −0.002 | 0.033 | −0.038 | −0.001 | 0.015 | 0.026 | 0.009 | 0.028 |
| 0.068 | 0.109 | 0.070 | 0.070 | 0.394 | 0.071 | 0.069 | 0.092 | 0.070 | |
| 0.067 | 0.112 | 0.067 | 0.070 | 0.388 | 0.068 | 0.068 | 0.089 | 0.068 | |
| Cov90 | 0.851 | 0.911 | 0.836 | 0.842 | 0.896 | 0.877 | 0.867 | 0.892 | 0.854 |
| Cov95 | 0.922 | 0.949 | 0.915 | 0.912 | 0.944 | 0.929 | 0.924 | 0.933 | 0.923 |
Abbreviations: cor, correct; Cov90, coverage proportion of the 90% CI; Cov95, coverage proportion of the 95% CI; mis, misspecified; OR, outcome regression; PS, propensity score; Var, variance.
Reproduced from Tan Z. Ann Statist. 2020;48:811-837.
Reprinted with permission from Annals of Statistics (Copyright ©2020). Institute of Mathematical Statistics. All Rights Reserved.
aRML denotes , and RML2 denotes the variant with and replaced by the fitted values obtained by refitting OR and PS models only including the variables selected from the corresponding Lasso estimation. RCAL denotes . Bias and Var are the Monte Carlo bias and variance of the points estimates. EVar is the mean of the variance estimates, and hence also measures the L2-average of lengths of CIs.
Table 2Estimates of 30-Day Survival Probabilities and ATEa
| IPW | Augmented IPW | |||||
|---|---|---|---|---|---|---|
| RML | RML2 | RCAL | RML | RML2 | RCAL | |
| μ1 | 0.636 ± 0.026 | 0.660 ± 0.049 | 0.634 ± 0.023 | 0.636 ± 0.021 | 0.646 ± 0.035 | 0.635 ± 0.021 |
| μ0 | 0.690 ± 0.017 | 0.691 ± 0.019 | 0.687 ± 0.017 | 0.691 ± 0.016 | 0.693 ± 0.018 | 0.688 ± 0.016 |
| ATE | −0.054 ± 0.031 | −0.031 ± 0.053 | −0.053 ± 0.029 | −0.055 ± 0.025 | −0.047 ± 0.039 | −0.053 ± 0.025 |
Abbreviations: ATE, average treatment effect; IPW, inverse probability weighting.
aEstimate ±2 × SE, including nominal SEs for IPW. RML denotes , and RML2 denotes the variant witb and replaced by the fitted values obtained by refitting OR and PS models only including the variables selected from the corresponding Lasso estimation. RCAL denotes .
Table 3Summary of Results for Estimation of θ1a
| (C1) cor IPS, more cor OR | (C2) cor IPS, less cor OR | (C3) mis IPS, more cor OR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RCAL | RML | RML2 | RCAL | RML | RML2 | RCAL | RML | RML2 | |
| (M1) n = 800 and p = 400 | |||||||||
| Bias | −0.146 | −0.195 | −0.007 | −0.054 | −0.208 | −0.118 | 0.043 | −0.022 | 0.119 |
| 0.433 | 0.435 | 0.896 | 0.518 | 0.521 | 1.231 | 0.429 | 0.434 | 0.804 | |
| 0.418 | 0.400 | 2.533 | 0.510 | 0.486 | 11.410 | 0.418 | 0.422 | 0.957 | |
| Cov90 | 0.854 | 0.811 | 0.868 | 0.889 | 0.830 | 0.848 | 0.886 | 0.876 | 0.885 |
| Cov95 | 0.908 | 0.889 | 0.930 | 0.935 | 0.897 | 0.898 | 0.932 | 0.933 | 0.939 |
| (M2) n = 800 and p = 400 | |||||||||
| Bias | −0.155 | −0.201 | −0.026 | −0.056 | −0.210 | −0.143 | 0.025 | −0.026 | 0.120 |
| 0.432 | 0.438 | 0.752 | 0.522 | 0.521 | 1.301 | 0.427 | 0.433 | 0.784 | |
| 0.415 | 0.401 | 1.290 | 0.509 | 0.486 | 11.804 | 0.415 | 0.422 | 0.790 | |
| Cov90 | 0.848 | 0.803 | 0.872 | 0.884 | 0.832 | 0.851 | 0.884 | 0.877 | 0.883 |
| Cov95 | 0.909 | 0.882 | 0.928 | 0.933 | 0.895 | 0.894 | 0.937 | 0.929 | 0.941 |
| (M1) n = 800 and p = 1000 | |||||||||
| Bias | −0.198 | −0.239 | −0.145 | −0.087 | −0.227 | −0.204 | 0.047 | −0.028 | 0.092 |
| 0.428 | 0.424 | 0.632 | 0.518 | 0.521 | 0.749 | 0.438 | 0.451 | 0.961 | |
| 0.411 | 0.393 | 0.600 | 0.439 | 0.477 | 0.742 | 0.411 | 0.413 | 0.816 | |
| Cov90 | 0.837 | 0.808 | 0.832 | 0.879 | 0.831 | 0.833 | 0.882 | 0.864 | 0.857 |
| Cov95 | 0.900 | 0.869 | 0.901 | 0.933 | 0.888 | 0.899 | 0.945 | 0.924 | 0.920 |
| (M2) n = 800 and p = 1000 | |||||||||
| Bias | −0.223 | −0.242 | −0.146 | −0.099 | −0.227 | −0.205 | 0.011 | −0.030 | 0.068 |
| 0.430 | 0.424 | 0.632 | 0.515 | 0.520 | 0.759 | 0.441 | 0.450 | 0.714 | |
| 0.407 | 0.393 | 0.605 | 0.491 | 0.476 | 0.744 | 0.407 | 0.412 | 0.677 | |
| Cov90 | 0.820 | 0.803 | 0.831 | 0.874 | 0.824 | 0.828 | 0.875 | 0.862 | 0.858 |
| Cov95 | 0.880 | 0.868 | 0.900 | 0.929 | 0.888 | 0.894 | 0.939 | 0.928 | 0.917 |
Abbreviations: cor, correct; Cov90, coverage proportion of the 90% CI; Cov95, coverage proportion of the 95% CI; EVar, estimated variance; IPS, instrument propensity score model; M, model; mis, misspecified; OR, outcome and treatment regression models; Var, variance.
aRCAL denotes , RM L denotes , and RML2 denotes the variant where the nuisance parameters are estimated by refitting models with only the variables selected from the corresponding Lasso estimation. Bias and are the Monte Carlo bias and SD of the point estimates, and is the square root of the mean of the variance estimates. Cov90 and Cov95 are based on 1000 repeated simulations. The true values of under (C1) to (C3) are calculated using Monte Carlo integration with 100 repeated samples each of size 107.
Table 4Estimates of the Effect of Education Beyond High School on Log of Earningsa
| RCAL | RML | RML2 | |
|---|---|---|---|
| Nonpenalized main effects (p = q1 = 19, q2 = 21) | |||
| θ 0 | 6.565 ± 0.236 | 6.609 ± 0.274 | — |
| θ 1 | 6.402 ± 0.297 | 6.307 ± 0.348 | — |
| LATE | 0.164 ± 0.365 | 0.302 ± 0.439 | — |
| Linear spline with 3 knots (p = q1 = 114, q2 = 122) | |||
| θ 0 | 6.665 ± 0.346 | 6.608 ± 0.310 | 6.582 ± 0.364 |
| θ 1 | 6.269 ± 0.382 | 6.263 ± 0.365 | 6.256 ± 0.406 |
| LATE | 0.396 ± 0.535 | 0.346 ± 0.480 | 0.326 ± 0.538 |
| Linear spline with 9 knots (p = q1 = 213, q2 = 233) | |||
| θ 0 | 6.675 ± 0.318 | 6.627 ± 0.315 | 6.586 ± 0.351 |
| θ 1 | 6.197 ± 0.359 | 6.234 ± 0.358 | 6.196 ± 0.400 |
| LATE | 0.478 ± 0.505 | 0.393 ± 0.479 | 0.390 ± 0.533 |
| Linear spline with 15 knots (p = q1 = 312, q2 = 344) | |||
| θ 0 | 6.684 ± 0.310 | 6.625 ± 0.310 | 6.584 ± 0.341 |
| θ 1 | 6.180 ± 0.360 | 6.226 ± 0.359 | 6.195 ± 0.394 |
| LATE | 0.504 ± 0.498 | 0.400 ± 0.476 | 0.389 ± 0.522 |
Abbreviation: LATE, local average treatment effect.
aEstimate ± 1.96 × SE. The number of regressors is indicated by p, q1 or q2 in the instrument PS, treatment regression, or model. RCAL denotes , RM L denotes , and RML2 denotes the variant where the nuisance parameters are estimated by refitting models with only the variables selected from the corresponding Lasso estimation.
Suggested citation:
Tan Z, Gerhard T, Sun B. (2022). Developing and Testing New Methods for Estimating Treatment Effectiveness in Observational Studies Using High-Dimensional Data (PCORI). http://doi.org/10.25302/11.2021.ME.151132740
Disclaimer
The [views, statements, opinions] presented in this report are solely the responsibility of the author(s) and do not necessarily represent the views of the Patient-Centered Outcomes Research Institute® (PCORI®), its Board of Governors or Methodology Committee.