Abstract
The N-methyl-D-aspartate subfamily of ionotropic glutamate receptors (NMDARs) is well known for its important roles in the central nervous system (CNS), e.g. learning and memory formation. Besides the CNS, NMDARs are also expressed in numerous peripheral tissues including the pancreas, kidney, stomach, and blood cells, where an understanding of their physiological and pathophysiological roles is only evolving. Whereas subunit composition increases functional diversity of NMDARs, a great number of endogenous cues tune receptor signaling. Here, we characterized the effects of the steroid bile salts cholate and chenodeoxycholate (CDC) on recombinantly expressed NMDARs of defined molecular composition. CDC inhibited NMDARs in an isoform-dependent manner, preferring GluN2D and GluN3B over GluN2A and GluN2B receptors. Determined IC50 values were in the range of bile salt serum concentrations in severe cholestatic disease states, pointing at a putative pathophysiological significance of the identified receptor modulation. Both pharmacological and molecular simulation analyses indicate that CDC acts allosterically on GluN2D, whereas it competes with agonist binding on GluN3B receptors. Such differential modes of inhibition may allow isoform-specific targeted interference with the NMDAR/bile salt interaction. In summary, our study provides further molecular insight into the modulation of NMDARs by endogenous steroids and points at a putative pathophysiological role of the receptors in cholestatic disease.
Subject terms: Physiology, Gastroenterology
Introduction
N-methyl-D-aspartate receptors (NMDARs) comprise a subfamily of ionotropic glutamate receptors (iGluRs). NMDARs assemble from combinations of GluN1, GluN2 and GluN3 subunits, whereby they build tetrameric ion channels, with GluN1 being obligatory for channel function. Distinct from other iGluR subfamilies, most NMDARs show significant Ca2+ permeability and exhibit an apparent voltage-dependence due to voltage-dependent block by extracellular Mg2+ ions1,2. Activation of most NMDAR subunit combinations requires binding of the agonist glutamate to GluN2 and the co-agonists glycine or D-serine to GluN1 subunits3. The exceptions are channels assembled from GluN1 and GluN3, which lack a glutamate-binding site and hence serve as glycine-activated cation channels4. Aside from their well-characterized expression in the brain, both in neuronal and non-neuronal cells, NMDARs have been identified in a number of peripheral tissues and systems5. These include circulating blood cells such as lymphocytes and platelets, which may employ NMDARs for cell activation. As non-neuronal NMDARs are presumably directly exposed to high levels of plasma glutamate, alternative agonists such as L-homocysteic acid (L-HCA) and quinolinic acid (QN) are discussed as receptor ligands5.
NMDAR activity is modulated by numerous endogenous cues including pH, metal ions, polyamines, and lipids6. Neurosteroids derived from the cholesterol backbone may allosterically either potentiate or inhibit NMDAR function in an isoform-dependent manner6–9. The main steroid salts contained in human bile, cholate and chenodeoxycholate (CDC), are also derived from cholesterol. These primary bile salts are synthesized by hepatocytes, conjugated to glycine or taurine to increase water solubility, and finally secreted into the intestine to help emulsifying food lipids. Bile salts are efficiently reabsorbed from the intestine and transported back to the liver for reuse by the hepatic portal system (enterohepatic cycle). Under physiological conditions, only insignificant amounts of bile salts enter systemic circulation. In certain cholestastic disease states like progressive familial forms of intrahepatic cholestasis or severe forms of it in pregnancy or acute hepatitis, however, plasma concentrations of bile salts may rise to hundred µM and more10–12. When applied to neurons, cholate and CDC block NMDA receptors13 and it is known that CDC can improve neurological symptoms of cerebrotendinous xanthomatosis, a disorder of bile salt metabolism14. Another bile salt, tauroursodeoxycholate, is neuroprotective on NMDA-induced retinal ganglion cell degeneration15. Furthermore, NMDA receptors are reported to be involved in modulation of cholestasis-induced antinociception in rat16,17 and there is a potential involvement of the dorsal hippocampal (CA1) glutamatergic system in cholestasis-induced decrease in rats’ memory function18. Thus, bile salt effects on NMDA receptors can have a physiological and pathophysiological relevance in nervous system or peripheral tissues.
Here, we have studied the effects of the most common human bile salts, cholate and CDC, on NMDARs of different subunit composition. We demonstrate that bile salts inhibit NMDARs in an isoform-specific manner, both with respect to efficacy and to the molecular mechanism of action. Our data shed new light on the effects of bile salts in cholestatic diseases as well as when used in therapy.
Results
CDC inhibits preferentially the GluN subtypes 2D and 3B
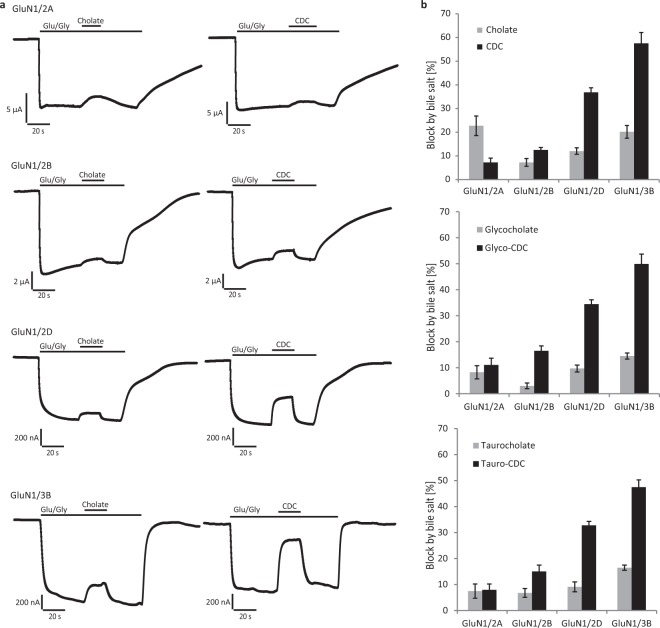
The effects of the bile salts cholate and CDC on GluNs were probed on recombinant receptors of defined subunit composition expressed in Xenopus laevis oocytes. For initial experiments, agonists were applied at saturating concentration to ensure maximum activation of GluN2A, GluN2B, GluN2D, and GluN3B, respectively4,19. Cholate inhibited steady-state currents only moderately irrespective of receptor subtype, while CDC was more potent and reduced preferentially GluN2D and GluN3B currents (Fig. 1, Table S1). Inhibition by 100 µM CDC ranged between 7 ± 2% of GluN2A and 13 ± 1% of GluN2B steady-state currents, whereas it amounted to 37 ± 2% of GluN2D and even to 58 ± 5% of GluN3B currents. The bile salt effects were specific for GluNs, as no inhibition of glutamate-induced steady-state kainate receptor GluK2 current (n = 3, after block of desensitization with ConA) and only a minor reduction of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor GluA1/GluA2 currents (7 ± 1%, n = 6) were observed after application of 100 µM CDC. Somewhat unexpected, taurine or glycine conjugation of bile salts did neither change their overall potencies in inhibiting GluNs nor their subunit preferences.
Figure 1.
Inhibition of NMDARs by the bile salts cholate and CDC. (a) Representative current traces recorded from Xenopus laevis oocytes expressing NMDARs of indicated molecular compositions. Note the reversible reduction of agonist-induced currents by cholate and CDC. (b) Quantification of the experiments in (a). Given is the mean reduction (±SEM) of indicated NMDAR currents by application of 100 μM bile salts (in % of steady-state agonist-induced current, n = 6–14 oocytes). Glutamate (Glu): 150 µM, Glycine (Gly): 10 µM.
Allosteric inhibition of GluN2D by tauro-CDC
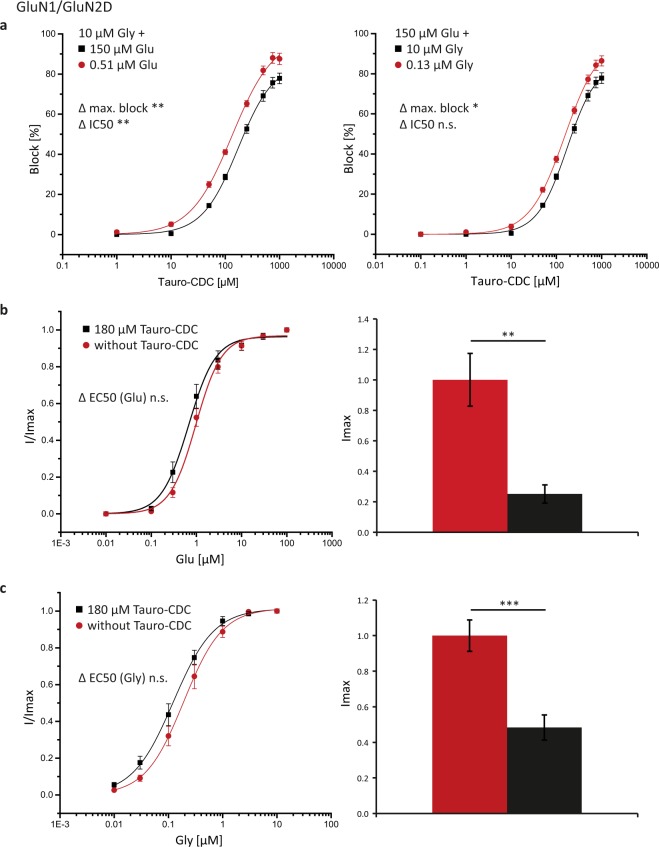
To dissect the mechanism of GluN2D inhibition by bile salts, we recorded dose-response relations for CDC at both saturating and EC50 NMDAR agonist concentrations20,21. We used routinely taurine-conjugated CDC in these experiments, because of higher water solubility and hence more feasible handling.
As depicted in Fig. 2a, maximum inhibition of glutamate/glycine-induced currents by tauro-CDC was significantly smaller at saturating than at EC50 agonist concentrations (n = 8–13; p = 0.01 and 0.03 for glutamate and glycine, respectively).
Figure 2.
Tauro-CDC inhibits GluN2D receptors in an allosteric manner. (a) Concentration-response curves for inhibition of GluN1/GluN2D receptors by tauro-CDC at saturating (squares) and half-maximum (dots) agonist concentrations (glutamate/glycine, Glu/Gly) as indicated20,21. Displayed is mean ± SEM of recordings from n = 8–13 oocytes. (b) Concentration-response curves (left) and maximum currents (right) induced by the agonist Glu in the presence (squares) and absence (dots) of 180 µM tauro-CDC. The concentration of the co-agonist Gly was kept constant at 10 µM. Displayed is the mean ± SEM of recordings from n = 7 oocytes. (c) Concentration-response curves and maximum currents induced by the co-agonist Gly in the presence (squares) and absence (dots) of 180 µM tauro-CDC. The concentration of the agonist Glu was kept constant at 150 µM. Displayed is the mean ± SEM of recordings from n = 12–13 oocytes. The results of t-tests are reported as follows: n.s. p > 0.05, *p ≤ 0.05, **p ≤ 0.01, ***p < 0.001.
Conversely, dose-response curves for glutamate and glycine in the absence or presence of 180 μM tauro-CDC, which was calculated to be the mean IC50 (179 ± 11 μM, n = 13, saturating agonist concentration), showed that the maximum agonist-induced currents were significantly reduced by the bile salt (Fig. 2b,c; n = 7–13, p = 0.0002 and 0.003 for glycine and glutamate, respectively). There were neither significant differences between the EC50 values for glutamate or glycine at varying concentrations of tauro-CDC (n = 7–13, p = 0.3 and 0.2 for glutamate and glycine respectively) nor were there different IC50 values for tauro-CDC at varying concentrations of glycine (n = 8–13; p = 0.1; Table S2). Only the IC50 value for tauro-CDC at the glutamate EC50 concentration was significantly smaller compared to inhibition at a saturating glutamate concentration (n = 11–13, p = 0.009).
Application of 100 µM tauro-CDC in the absence of NMDAR agonists showed no effects on GluN2D or GluN3B receptors (n = 4) excluding partial agonist action of bile salts on NMDA receptors (data not shown). Taken together, these results strongly suggest that tauro-CDC inhibits GluN2D receptors by an allosteric mechanism.
Competitive inhibition of GluN3B by tauro-CDC
Next, we sought to investigate the mechanism of action of tauro-CDC-mediated inhibition of GluN3B receptors. As depicted in Fig. 3a, the mean IC50 for tauro-CDC was significantly higher in the presence of 10 μM glycine than in the presence of 5 μM glycine (83 ± 8 μM vs. 44 ± 7 μM, n = 6, p = 0.007). The maximum block by tauro-CDC, however, did not depend on the glycine concentration (95 ± 3% vs. 92 ± 3%, n = 6, p = 0.5). These data indicate that tauro-CDC inhibits GluN3B receptors – other than GluN2D receptors – in a competitive manner. We also recorded glycine dose-response curves in the presence or absence of 100 μM tauro-CDC (n = 6–11, Fig. 3b). Known receptor desensitization at higher glycine concentrations prevented calculation of precise EC50 values4,22. However, as depicted in Fig. 3b, the bell-shaped concentration-response curve shifted to higher glycine concentrations in the presence of tauro-CDC.
Figure 3.
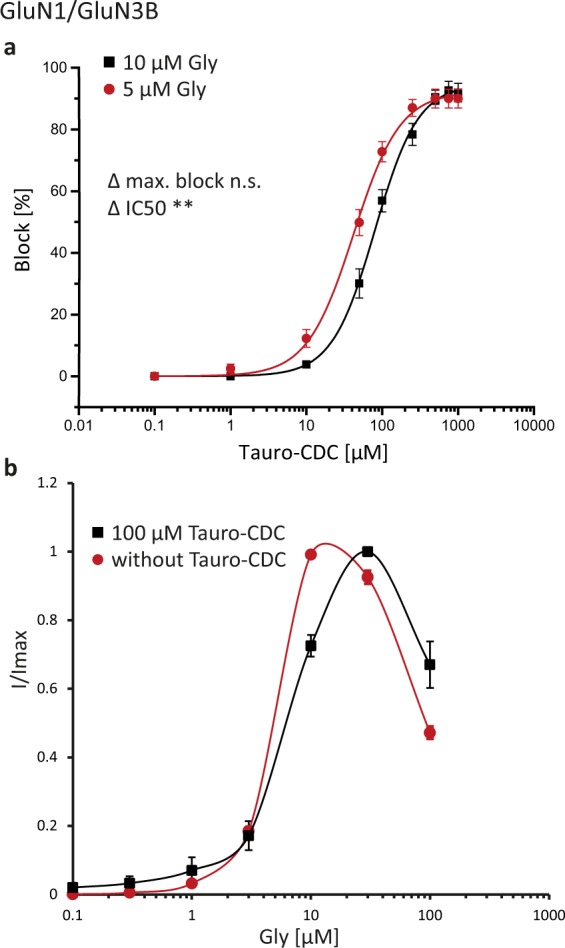
Tauro-CDC inhibits GluN3B receptors in a competitive manner. (a) Concentration-response curves for inhibition of GluN1/GluN3B receptors by tauro-CDC at saturating (squares) and estimated half-maximum (dots) glycine (Gly) concentrations as indicated4. Displayed is mean ± SEM of recordings from n = 6 oocytes. (b) Concentration-response curves for Gly in the presence or absence of 100 μM Tauro-CDC (n = 6–11 oocytes). The results of t-tests are reported as follows: n.s. p > 0.05, *p ≤ 0.05, **p ≤ 0.01, ***p < 0.001.
Tauro-CDC has no effect on ion selectivity
Bile salts are known to integrate into the plasma membrane of cells23, which might impact ion channel pores including their selectivity filters. Therefore, we checked for potential bile salt effects on GluN receptor ion selectivity. Current-voltage (I/V) relationships of agonist-induced currents were recorded for GluN2D and GluN3B in the absence and presence of 100 µM tauro-CDC (n = 10–11). For better comparison of I/V curves, individual oocyte data were normalized to their maximum inward current at −140 mV. As shown in Fig. 4, tauro-CDC did neither change the shape of I/V relationships nor did it shift the reversal potentials of the receptor currents. These results render a change in ion selectivity of the two GluNs by bile salts unlikely.
Figure 4.
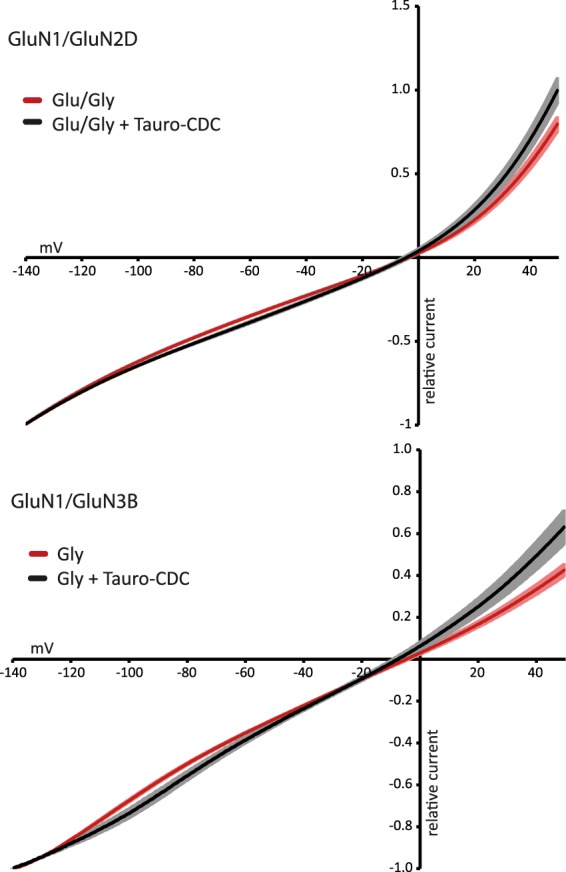
Tauro-CDC does not affect the ion selectivity of NMDARs. I/V relationships (n = 10–11, mean ± SEM) for indicated NMDARs of agonist-induced currents in presence (black) and absence (red) of 100 μM tauro-CDC. Data were normalized to maximum inward current at –140 mV. Note that the reversal potentials do not change in the presence of tauro-CDC.
Bile salt inhibition of GluNs when activated by alternative agonists
As the inhibition of GluNs by bile salts required concentrations that are hardly reached in the CNS, we tested whether tauro-CDC also reduced currents elicited by the alternative non-neuronal NMDAR agonists L-homocysteic acid (L-HCA) and quinolinic acid (QN)5.
As shown in Fig. 5, GluN2D currents induced by application of L-HCA at its reported EC50 of 13 µM24 were blocked by 30 ± 2% (n = 12), whereas currents elicited by QN at its reported EC50 of 7.2 mM24 were reduced by 26 ± 2% (n = 7) when co-applying tauro-CDC at 100 µM. Lowering the agonist concentration of QN to 1 mM did not change inhibition by tauro-CDC, which was still 29 ± 2% (n = 7). For all these experiments involving the non-neuronal NMDAR agonists L-HCA and QN on GluN2D receptors, 10 µM glycine was used as co-agonist. GluN3B could not be activated by L-HCA, even at high concentrations of up to 1 mM (n = 4). In contrast, currents activated by 7.2 mM QN were reduced by about 68 ± 4% (n = 5), with QN showing no effect on uninjected oocytes (n = 3).
Figure 5.
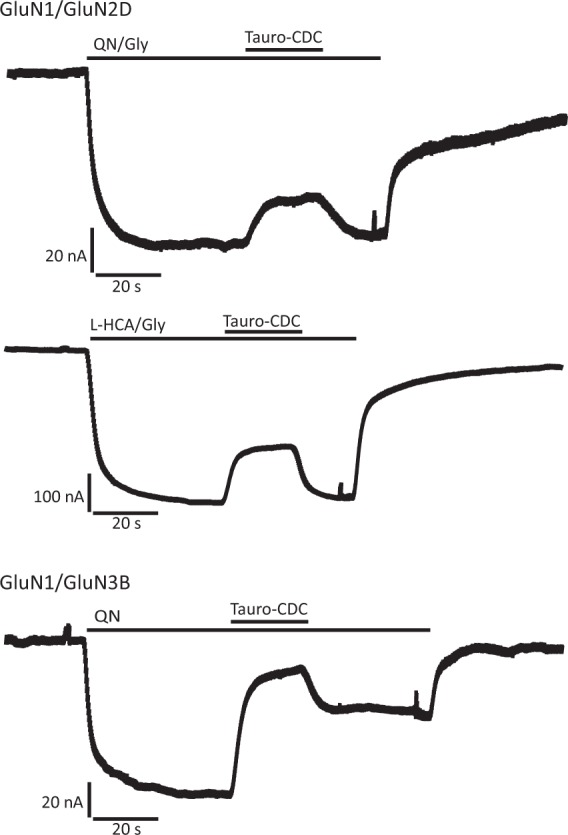
Bile salt inhibition of NMDARs activated by the alternative agonists quinolinic acid (QN) and L-homocysteic acid (L-HCA). Representative current traces recorded from Xenopus laevis oocytes expressing NMDARs of indicated molecular compositions. Note the reversible reduction of currents induced by QN (7.2 mM) and L-HCA (13 µM) by tauro-CDC (100 µM). Concentrations of QN and L-HCA are reported EC5024.
Binding modes of tauro-CDC in GluN2DLBD and GluN3BLBD
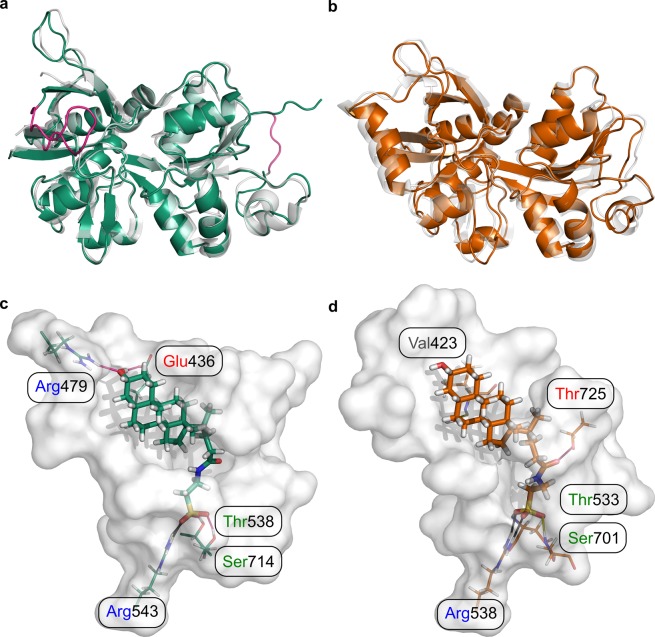
The pharmacological experiments indicated that tauro-CDC acts as a non-competitive allosteric antagonist of GluN2D, but as a competitive antagonist of GluN3B. In order to assess the molecular origin of isoform-specific inhibition of NMDARs by tauro-CDC, we performed induced fit docking experiments of tauro-CDC in respective ligand binding domains (LBDs) of the NMDAR isoforms (Fig. 6a,b), which allows to consider receptor flexibility in terms of side chain rearrangements.
Figure 6.
Homology models of GluN2DLBD and GluN3BLBD and docking-derived complex structures with tauro-CDC. (a) Homology model of GluN2DLBD (green). The loop consisting of residues 464–476 (magenta, left) was modeled de novo due to its absence in the template structure (grey, PDB ID: 3OEK45). The engineered Gly-Thr linker in the template structure (magenta, right) was removed in the final model. (b) Homology model of GluN2DLBD (orange) superimposed onto the template structure (grey, PDB ID: 2RCA32). (c) Binding mode of tauro-CDC (green sticks) in GluN2DLBD (white surface) predicted by docking. Residues involved in hydrogen bonds and salt bridges are depicted as lines. Positively and negatively charged residues are labeled in blue and red, respectively. Polar residues are labeled in green. (d) Binding mode of tauro-CDC (orange sticks) in GluN3BLBD (white surface) predicted by docking. Residues involved in hydrogen bonds and salt bridges are depicted as lines. Positively and negatively charged residues are labeled in blue and red, respectively. Polar residues are labeled in green and hydrophobic residues are labeled in grey.
For both GluN2DLBD and GluN3BLBD, binding modes of tauro-CDC (Fig. 6c,d) were predicted with similar docking scores (IFDScore25) of ~7.4 kcal·mol−1. In agreement, both binding modes were of similar geometry with an in-place root-mean-square deviation (RMSD) of the ligand atoms of 2.98 Å after superimposition of the Cα atoms of the protein structures (RMSD: 1.45 Å). The similarity in binding mode geometry was paralleled by a similar interaction profile in both complexes (Fig. 6c,d).
Hence, the static structures obtained from docking experiments cannot explain the observed isoform specificity of NMDAR inhibition by tauro-CDC.
Structural variability of tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD binding modes
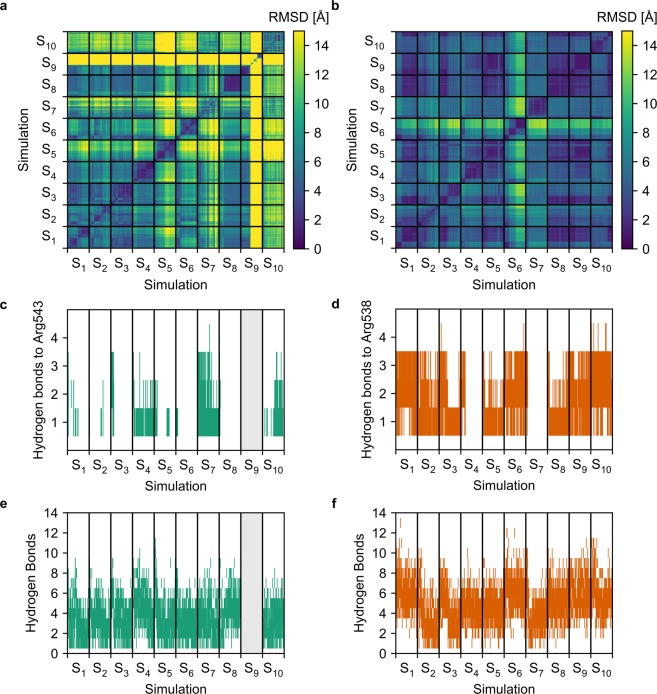
We next asked whether the predicted binding modes of tauro-CDC in GluN2DLBD or GluN3BLBD structurally vary over time scales accessible by molecular dynamics (MD) simulations. We therefore carried out ten MD simulations (S1-S10) of 500 ns length each for both the tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD systems and quantified the structural deviation from the initial tauro-CDC pose within each simulation and between independent simulations. Similarly, we quantified the conformational variability of tauro-CDC to account for potential alternative binding modes.
Taking all simulations but S9 into account, the average RMSD of the tauro-CDC pose in GluN2DLBD was 2.86 ± 0.35 Å higher than in GluN3BLBD (Supplementary Fig. 3a). Simulation S9 of GluN2DLBD was omitted from this and all subsequent analyses when tauro-CDC unbound after ~225 ns (Supplementary Fig. 3b). No unbinding event was observed in the simulations of tauro-CDC/GluN3BLBD.
The average pairwise RMSD of the tauro-CDC pose of all snapshots extracted from the MD simulations was 8.44 ± 0.001 Å for tauro-CDC/GluN2DLBD (Figs. 7a) and 4.82 ± 0.001 Å for tauro-CDC/GluN3BLBD (Fig. 7b). Taking the quadratic mean of the pairwise RMSD as a measure for pose diversity26 revealed that the tauro-CDC poses observed both within and between simulations were substantially more diverse in GluN2DLBD systems (mean: 8.43 ± 0.46 Å, Supplementary Fig. 3c) than in GluN3BLBD systems (mean: 4.89 ± 0.26 Å, Supplementary Fig. 3d) (t(98) = 7.01, p < 10–4).
Figure 7.
Structural variability and number of hydrogen bonds in the tauro-CDC-GluN2DLBD and tauro-CDC-GluN3BLBD complexes during the MD simulations. (a) Two-dimensional root-mean-square deviation (RMSD) of the atomic positions of tauro-CDC after least squares fitting of the Cα atom coordinates of the GluN2DLDB in all 10 MD simulations. (b) Two-dimensional root-mean-square deviation (RMSD) of the atomic positions of tauro-CDC after least squares fitting of the Cα atom coordinates of the GluN3BLDB in all 10 MD simulations. (c) Number of hydrogen bonds between tauro-CDC and Arg543 in GluN2DLBD over the course of 10 MD simulations. (d) Number of hydrogen bonds between tauro-CDC and Arg538 in GluN3BLBD over the course of 10 MD simulations. (e) Total humber of hydrogen bonds between tauro-CDC and GluN2DLBD over the course of 10 MD simulations. (f) Total number of hydrogen bonds between tauro-CDC and GluN3BLBD over the course of 10 MD simulations. In panels c and e, data for MD simulation S9 is not shown because here tauro-CDC unbinds after 225 ns (c.f. Supplementary Fig. 3b), and the corresponding data was excluded from statistical analysis.
To conclude, these results reveal that the predicted binding mode of tauro-CDC in GluN2DLBD is structurally less stable than in GluN3BLBD. In one simulation of tauro-CDC in GluN2DLBD, tauro-CDC even unbound. Note that simulating ligand unbinding events is challenging also for ligands with moderate affinities due to low off-rates27, which may explain why the unbinding occurred only in one simulation. As to GluN3BLBD, the results are in line with our experimental data, according to which tauro-CDC must bind to the glycine binding site in order to competitively inhibit GluN3B-containing NMDARs.
Contributions of hydrogen bonds to tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complex stability
To assess whether a difference in structural variability between tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD may be attributed to differences in intermolecular interactions within the complexes, we quantified the amount of hydrogen bonds formed between tauro-CDC and an arginine residue that is crucial for binding of the agonist glutamate to GluN2DLBD (Arg543) and of glycine to GluN3BLBD (Arg538) over the course of all MD simulations. Additionally, we quantified the total amount of hydrogen bonds between tauro-CDC and GluN2DLBD or GluN3BLBD. We focused here on identifying hydrogen bonds as interactions that contribute to the stability of the tauro-CDC/GluN3BLBD complex in order to predict mutations for ex vivo validation of a suggested tauro-CDC binding mode.
The average hydrogen bond count between Arg543 in GluN2DLBD and tauro-CDC was 0.31 ± 0.01 (Fig. 7c). In contrast, Arg538 in GluN3BLBD formed hydrogen bonds to tauro-CDC about four times more frequently (mean: 1.31 ± 0.01) (t(9498) = 58.58, p < 10−4) (Fig. 7d). Similarly, the average number of hydrogen bonds formed between the complete GluN2DLBD and tauro-CDC (mean: 3.58 ± 0.03) (Fig. 7e) was significantly lower than the average number of hydrogen bonds formed between the complete GluN3BLBD and tauro-CDC (mean: 4.97 ± 0.03) (t(9498) = 38.10, p < 10−4) (Fig. 7f).
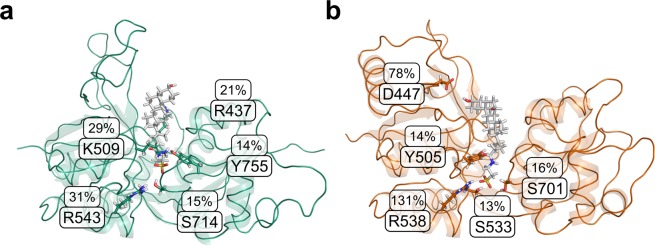
At a per-residue level, Arg543 showed the largest hydrogen bond occupancy (31%) for tauro-CDC/GluN2DLBD (Fig. 8a). The corresponding residue in GluN3BLBD (Arg538) displayed an occupancy of 131% (occupancy may exceed 100% as an arginine side chain can form more than one hydrogen bond) (Fig. 8b). Tauro-CDC in GluN3BLBD also formed a hydrogen bond with the 3α-OH group of the cholane scaffold to Asp447 (78% occupancy). This residue has no counterpart in the GluN2D sequence (Supplementary Fig. 1). In addition to Arg538 and Asp447, Ser701 (16%), Tyr505 (14%), and Ser533 (13%) were among the five residues that most frequently formed hydrogen bonds to tauro-CDC during the GluN3BLBD simulations (Fig. 8b). Lys509 (29%), Arg437 (21%), Ser714 (15%) and Tyr755 (14%) additionally stabilized the GluN2DLBD-tauro-CDC complex.
Figure 8.
Formation of protein-ligand hydrogen bonds during the MD simulations. Average hydrogen bond occupancy of the five amino acids most frequently involved in hydrogen bonding to tauro-CDC in (a) the 9 tauro-CDC-GluN2DLBD simulations and (b) the 10 tauro-CDC-GluN3BLBD simulations.
To conclude, hydrogen bond formation between tauro-CDC and Arg543 in GluN2DLBD occurred less frequently than between tauro-CDC and Arg538 in GluN3BLBD; the same held true when considering hydrogen bond formation to the complete LBD. The tauro-CDC/GluN3BLBD complex was particularly stabilized by Arg538 and, to a lesser extent, Asp447, whereas no particular amino acid contributed to stabilizing tauro-CDC/GluN2DLBD.
Effective binding energies of tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complexes
To complement our findings from the structural analysis of tauro-CDC complexes, we quantified the effective binding energy of tauro-CDC to GluN2DLBD or GluN3BLBD with the end-point effective energy approaches MM/PBSA and MM/GBSA.
The effective binding energy computed by MM/GBSA for tauro-CDC/GluN2DLBD (mean: −33.53 ± 0.67 kcal·mol−1) was significantly less negative than for tauro-CDC/GluN3BLBD (mean: −48.90 ± 0.62 kcal·mol−1) (t(17) = 16.84, p < 10−4) (Fig. 9d). The same trend was obtained with the MM/PBSA approach (tauro-CDC/GluN2DLBD: mean: −27.14 ± 0.52 kcal·mol−1; tauro-CDC/GluN3BLBD: mean: −30.54 ± 0.63 kcal·mol−1; t(17) = 4.07, p = 8·10−4). The trend was stable irrespective of using a dielectric constant of the solute of ε = 1 (values above; Fig. 9a,d) or 4 (tauro-CDC/GluN2DLBD: mean: −43.98 ± 0.24 kcal·mol−1; tauro-CDC/GluN3BLBD: mean: −45.45 ± 0.22 kcal·mol−1; t(17) = 4.49, p = 3·10−4) (Fig. 9d); higher dielectric constants have been used before to account for highly charged binding sites28, as given in the case of the LBDs.
Figure 9.
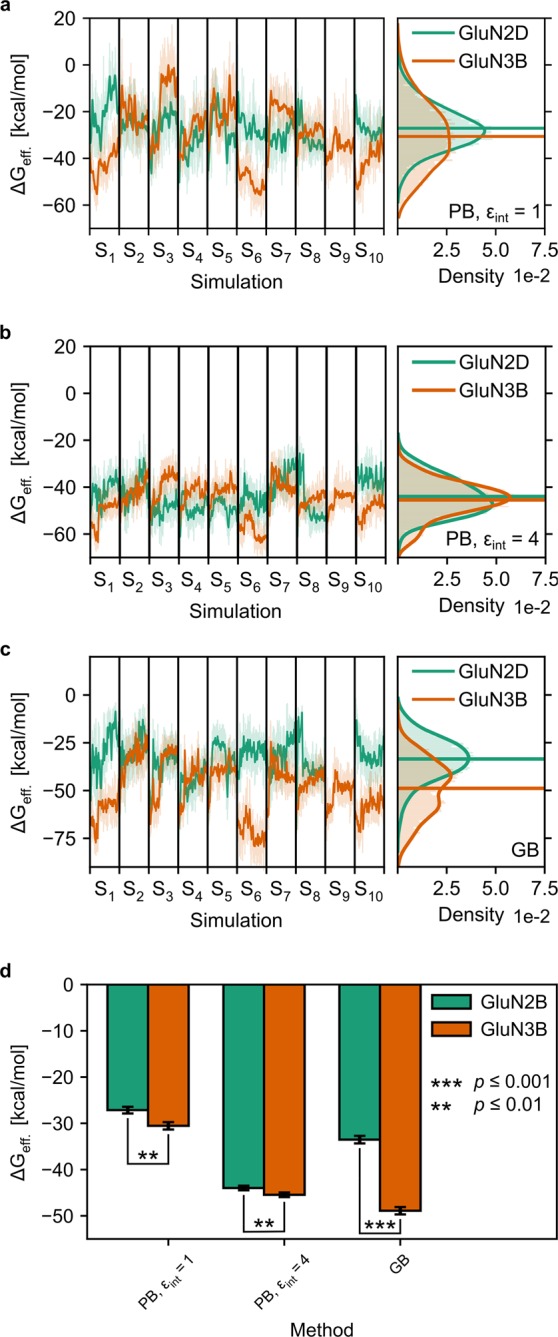
Effective binding energies (ΔGeff) of the tauro-CDC-GluN2DLBD (green) and tauro-CDC-GluN3BLBD (orange) complexes. (a–c) Time courses (left) and probability distributions (right) of ΔGeff, calculated using either the MM-PBSA method and an internal dielectric constant of (a) εint = 1 or (b) εint = 4, or (c) the MM-GBSA method using the modified OBC model67. Thick, opaque lines in the time courses represent the data smoothed with a Savitzky-Golay filter (window length = 51, degree of the smoothing polynomial = 2); thin, transparent lines show the unsmoothed data. Thick, opaque lines in the probability distributions show the distribution calculated with a Gaussian core density estimator (bandwidth calculated using Scott’s rule72); thin, transparent lines show the underlying data as a histogram. (d) Time-averaged mean ΔGeff, calculated using either the MM-PBSA method and an internal dielectric constant of εint = 1 or εint = 4, or the MM-GBSA method using the modified OBC model67. In panels a-c, data for MD simulation S9 is not shown because here, tauro-CDC unbinds after 225 ns (c.f. Supplementary Fig. 3b), and the corresponding data was excluded from statistical analysis.
To conclude, both approaches revealed more negative effective energies of tauro-CDC binding to GluN3BLBD than to GluN2DLBD. Thus, they indicate a stronger binding of tauro-CDC to GluN3BLBD.
Identification of an alternative binding site in the GluN1LBD/GluN2DLBD interface
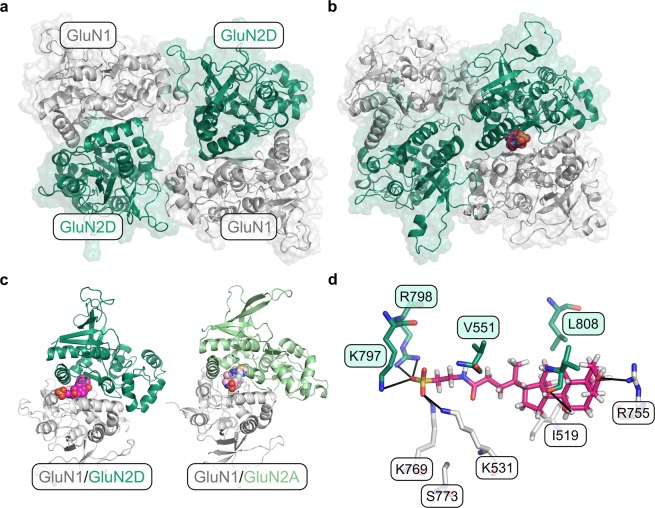
We further aimed to identify an alternative binding mode of tauro-CDC to a potentially allosteric site in the GluN1LBD/GluN2DLBD tetramer. To do so, we first detected potential binding pockets in a conformational ensemble obtained from 500 ns of accelerated MD simulations of the tetrameric GluN1LBD/GluN2DLBD interface (Fig. 10a) using the MDpocket software29. A single binding pocket at the GluN1/GluN2DLBD interface was identified, and tauro-CDC was docked into the receptor conformation in which the pocket showed the highest mean local hydrophobic density29,30 (Fig. 10b). The identified pocket largely overlaps with the allosteric binding pocket of the negative allosteric modulator MPX-007 in the GluN1/GluN2A interface31.
Figure 10.
Identification of a potentially allosteric binding site in the GluN1LBD/GluN2LBD interface. The GluN1 subunit is depicted in grey, the GluN2D subunit in dark green. (a) Initial model of the GluN1LBD/GluN2LBD tetramer. (b) Structure of the GluN1LBD/GluN2LBD tetramer in complex with tauro-CDC (magenta spheres). The ligand was docked to the pocket conformation that showed the highest mean local hydrophobic density29,30 during 500 ns of accelerated MD. (c) Structural comparison of the tauro-CDC-bound GluN1LBD/GluN2DLBD interface (left) and the crystal structure of the MPX-007-bound GluN1LBD/GluN2ALBD interface (right, PBD-ID: 5JTY31). The ligands are depicted as magenta and pink spheres, respectively. (d) Binding mode of tauro-CDC (magenta sticks) in the alternative binding pocket. Amino acids that belong to the GluN1 or GluN2D subunit are shown as white or green sticks, respectively. Possible hydrogen bonds and salt bridges are depicted as black lines.
During 500 ns of conventional MD simulations, tauro-CDC displayed an average RMSD value of 1.90 ± 0.01 Å (2.17 ± 0.01 Å without fitting, calculated on the last 250 ns of the simulation), indicating a low structural variability of the predicted binding mode. The binding mode is stabilized by interactions of the acid moiety with the positively charged residues Lys531 and Lys769 in the GluN1 subunit and Lys797 and Arg798 in the GluN2D subunit (Fig. 10d); Leu808 in the GluN2D subunit makes a hydrophobic contact with the cholane scaffold (Fig. 10d). Functional data on GluN1/GluN2A NMDARs indicates that Phe754 in GluN1 and Val783 in GluN2A form a molecular switch that mediates allosteric inhibition31. The corresponding Leu808 in GluN2D may assume a similar role as Val783 in GluN2A.
These tetramer simulations suggest that the interface between the GluN1 and GluN2D subunit forms a transient pocket, to which tauro-CDC can bind.
Point mutants
In order to verify the interaction of tauro-CDC with residues of the GluN3B LBD, Arg538 would be the primary residue for mutation studies due to its pronounced involvement in hydrogen bonds with the bile salt (Fig. 8b). However, we did not mutate Arg538 because this residue is reported to be important for agonist binding32. Rather, we mutated Asp447, Tyr505, and Ser701 (Fig. 8b) that also engage in hydrogen bonds with the bile salt. Yet, as these interactions are transient and, hence, likely rather weak, a decrease in the extent of tauro-CDC block would indicate an interaction of the bile salt with the mutated residue, while no effect would not exclude such an interaction due to potential enthalpy-entropy compensation effects33.
Mutation of Asp447 to Ala or Arg had neither an effect on agonist-induced current amplitudes (n = 2-3 dose-response curves) nor on the extent of tauro-CDC block in comparison to wild type receptor block (100 µM tauro-CDC, n = 9–12 at 10 µM Gly, n = 9–10 at 5 µM Gly). Mutation of Tyr505 to an Ala resulted in GluN3B receptors that could not be activated by its agonist glycine anymore (n = 9). Mutation of Ser701 to Ala strongly reduced glycine-induced currents from 835 ± 85 nA (n = 30) to 106 ± 12 nA (n = 29). While we observed an increase of 15% in CDC and tauro-CDC block (both 100 µM) for this mutant (n = 11–13), which might indicate an influence on CDC and tauro-CDC binding, it may also well be due to reduced glycine binding.
To conclude, none of the mutants showed a significant influence on tauro-CDC block such that no further information about binding (or non-binding) of tauro-CDC to GluN3B LBD may be inferred.
Discussion
Here, we have shown that the bile salt CDC effectively inhibits NMDARs with a preference on GluN2D and GluN3B containing receptors. Neither did conjugation of CDC per se nor the type of conjugated amino salt – taurine or glycine – change the overall inhibitory potency of the bile salt or shift its subunit preference. Based on detailed pharmacological analyses and supported by MD experiments, we infer from our data that CDC inhibits NMDARs by different mechanisms that are allosteric inhibition of GluN2D and competitive block of GluN3B containing receptors.
The observed subtype preference of NMDAR inhibition by CDC is in good agreement with the one reported for structurally similar neurosteroids. Thus, pregnenolone sulfate has been shown to significantly potentiate GluN2A and GluN2B containing NMDARs but has much lower efficacy on GluN2C and GluN2D receptors6–9. Also, the apparent insignificance of amino acid conjugates in the interaction of bile salts with receptors is paralleled in CDC-mediated activation of the bile acid receptor TGR5, which does not discriminate between conjugation substrates34. Intriguingly, however, our pharmacological experiments indicated different modes of inhibition for different GluN subtypes by CDC: allosteric inhibition of GluN2D and competitive block of GluN3B. In line with this suggestion, MD simulations predicted less structural stability for tauro-CDC binding in the orthosteric pocket of GluN2DLBD than in the one of GluN3BLBD. Effective binding energy computations comparing tauro-CDC/GluN2DLBD with tauro-CDC/GluN3BLBD complexes performed by two different approaches consistently revealed more negative effective binding energies of tauro-CDC binding to GluN3BLBD than to GluN2DLBD, thus supporting stronger binding of tauro-CDC to GluN3BLBD.
Previous studies have shown that inclusion of configurational entropy is crucial for calculating absolute binding free energies35,36. In the present study, however, we were rather interested in relative binding free energies and, thus, decided to neglect contributions due to changes in the configurational entropy of the ligand or the receptor upon complex formation in order to avoid introducing additional uncertainty in the computations35,37,38. Finally, MD simulations of the GluN1LBD/GluN2DLBD tetramer suggested that the interface between the GluN1 and GluN2D subunit forms a transient pocket, to which tauro-CDC can bind, which may explain the allosteric mechanism of action in this GluN subtype. We selected this interfacial pocket based on a combined approach of geometry-based cavity detection and druggability prediction that has been shown to be able to successfully identify binding-competent pocket conformations from an MD ensemble29. Notably, the detected pocket largely overlaps with the binding site of the negative allosteric modulator MPX-007 in the GluN1/GluN2A interface29. In order to verify binding of tauro-CDC to the orthosteric pocket of GluN3BLBD but not GluN2DLBD, we quantified hydrogen bond formation between tauro-CDC and neighboring residues based on geometric criteria over the course of the MD simulations. The results show that hydrogen bonding occurred less frequently between tauro-CDC and the GluN2DLBD than between tauro-CDC and the GluN3BLBD, in agreement with the above structural and energetic analyses of MD simulations. The tauro-CDC/GluN3BLBD complex is predominantly stabilized by a hydrogen bond to Arg538 and, to a lesser extent, Asp447. Of the residues mutated to alanine in the GluN3BLBD, positions 505 and 701 resulted in GluN3B receptors that could either not or hardly be activated by glycine anymore. For Ser701, it was reported that it forms hydrogen bonds with the glycine carboxylate group32, so it is not surprising that mutation of this site affected channel function. Mutation of Asp447 to an Ala or Arg had neither an effect on agonist-induced current amplitudes nor on the extent of tauro-CDC block, which does not exclude that Asp447 interacts with tauro-CDC, as enthalpy-entropy compensation effects upon mutation may account for the loss of interaction in the mutant33. In particular, we speculate that the Asp447Ala mutation leads to a loss in binding enthalpy upon disruption of the tauro-CDC-4Asp47 hydrogen bond, but this loss in binding enthalpy could be compensated by both a gain in entropy of the ligand due to an increase in translational and rotational degrees of freedom and a gain in entropy of the receptor due to increased conformational freedom of the residues surrounding the mutation site. The latter effect might especially be relevant due to the stabilizing interaction between Asp447 and Arg474, which would break upon mutation of Asp447 to alanine. Similarly, in the Asp447Arg mutant, the interaction between tauro-CDC and receptor could be preserved if arginine acted as a hydrogen bond donor for the 3-OH group of tauro-CDC, which would in turn act as a hydrogen bond acceptor. Moreover, repulsive forces between Arg447 in the Arg447Arg mutant and Arg474 could lead to a gain in receptor entropy.
The inhibition of GluNs by bile salts required concentrations that are hardly reached in the CNS, where CDC and cholate exists in the nmol/g range39,40. However, NMDARs are also widely expressed in non-neural peripheral tissues. These receptors have many distinct physiological and pathophysiological roles, and there is evidence that peripheral NMDARs may use alternative agonists such as L-HCA and QN5. We could show that tauro-CDC also reduced currents elicited by these alternative NMDAR agonists, indicating potential modulation of peripheral NMDAR function by bile salts. Whereas under physiological conditions only low µM amounts of bile salts are present in serum and urine, in cholestatic disease states like inherited progressive cholestasis, severe forms of intrahepatic cholestasis of pregnancy or acute hepatitis, plasma concentrations may rise to hundred µM and more10–12. As blood cells including platelets express NMDARs, it may well be hypothesized that bile salt mediated receptor inhibition contributes to the reported platelet activation defects and impaired thrombus formation in cholestatic liver disease41. Despite the observed preference of bile salts for specific receptor isoforms, it remains difficult to predict the exact physiological or pathophysiological consequences of their action on NMDAR signaling. The net effect of bile salts on NMDARs will eventually depend on the overall expression, stoichiometric assembly, and posttranscriptional and posttranslational modifications of individual GluN isoforms in a given cell type42. On a pharmacological perspective, however, the distinct modes of NMDAR inhibition by bile salts, i.e. allosteric versus competitive, may be exploited for developing targeted interference strategies holding isoform specificity.
Materials and Methods
Molecular biology
The cDNAs coding for NMDA and kainate receptors, subcloned into pSGEM for expression in Xenopus laevis oocytes, were kindly provided by Michael Hollmann (Ruhr University Bochum). AMPA receptor cDNAs were inserted in pGEM-HE for cRNA synthesis. The following cDNAs were used: GluN1-1a (U08261), GluN2A (NM_012573), GluN2B (NM_012574), GluN2D (U08260), GluN3B (NM_130455), GluK2 (NM_019309), GluA1 (NM_031608) and GluA2 (M38061). These cDNAs are from rat except for GluN3B, which is from mouse. Point mutants were generated by polymerase chain reaction (PCR)-directed mutagenesis with specific mismatch primers (biomers.net). cRNA was synthesized from 1 µg of linearized plasmid DNA using an in vitro transcription kit (mMESSAGE mMACHINE® T7 Transcription Kit, Thermo Fisher Scientific).
Heterologous expression of iGluRs in Xenopus laevis oocytes
Oocytes were obtained from parts of the ovaries surgically removed from Xenopus laevis in accordance with German law and approved by the local authorities of the Heinrich Heine University of Düsseldorf. Lumps of around 20 oocytes were incubated with 10 mg/ml collagenase type 2 (Worthington Biochemical Corporation) for 1–1.5 h in Ca2+-free Barth’s solution (in mM: 88 NaCl, 1 KCl, 2.4 NaHCO3, 0.82 MgSO4, 20 HEPES, pH adjusted to 7.5 with NaOH) with slow agitation to remove the follicular cell layer and then washed extensively with Barth’s solution containing Ca2+ (in mM: 88 NaCl, 1 KCl, 2.4 NaHCO3, 0.82 MgSO4, 0.41 CaCl2, 0.33 Ca(NO3)2, 20 HEPES, pH adjusted to 7.5 with NaOH) to inactivate the collagenase. Oocytes were maintained in Barth’s solution charged with antibiotic and antimycotic solution (containing penicillin, streptomycin and amphotericin B, Sigma-Aldrich) at 18 °C. Alternatively, Xenopus laevis oocytes were purchased from EcoCyte Bioscience (Castrop-Rauxel, Germany). Within 24 h after surgery, oocytes of stages V-VI were injected with 3.8 ng GluN1 and 5 ng GluN2A or GluN2B cRNAs, 7.6 ng GluN1 and 10 ng GluN2D cRNA or 7.6 ng GluN1 and 6.4 ng GluN3B-cRNA per oocyte (molecular GluN1 to GluN2 ratio: 1:1; GluN1 to GluN3 ratio: 1:1) using a Micro4 nanoliter injector (World Precision Instruments, Sarasota, FL, USA).
Electrophysiological recordings
Two-electrode voltage clamp recordings of oocyte current responses were performed 3–5 days after cRNA injection at −70 mV holding potential with a Turbo Tec-03X amplifier (npi electronic, Germany) controlled by Pulse software (HEKA, Germany). Electrodes were filled with 3 M KCl and had resistances of 0.5–1.5 MΩ. Oocytes were continuously superfused with calcium-free Ba2+-Ringer’s solution (in mM: 115 NaCl, 2.5 KCl, 1.8 BaCl2 and 10 HEPES, pH 7.2) to prevent the activation of endogenous Ca2+-gated chloride channels. Agonists and bile salts were applied for 20–40 s by superfusion. Agonist and bile salt blocker potencies were determined by recording current responses induced by the application of increasing agonist concentrations or increasing bile salt concentration to the same oocyte. Agonist-induced currents were normalized to the maximum response under saturating agonist concentration. In case of inhibition by bile salts the relative reduction in agonist-induced current was determined. Data from each oocyte was fitted separately to the Hill equation using Origin 9 software. The resulting EC50 or IC50 values were averaged. Current-voltage relationships were determined by ramping the holding potential from −140 mV to +50 mV corrected for background conductivities. Data are reported as mean ± standard error of the mean (SEM). Statistical significance was determined using the unpaired, two-tailed Student’s t-test.
Molecular modeling and molecular dynamics simulations
Preparation of tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complex structures
In order to generate full-length structures of rat GluN2D and mouse GluN3B LBDs (from now on referred to as GluN2DLBD and GluN3BLBD), we first generated a multiple sequence alignment of all rat and mouse GluN1, GluN2, and GluN3 subunit sequences using the MAFFT43 server with default settings applied. The alignment was further refined using the GLProbs software44 with two passes of consistency transformation and 100 passes of iterative refinement. The resulting alignment was then used as a template to manually align the sequence portions resolved in the selected template structures for GluN2DLBD (PDB ID: 3OEK45) and GluN3BLBD (PDB ID: 2RCA32) to the target sequences using the BioLuminate package (Schrödinger Release 2018–3: BioLuminate, Schrödinger, LLC, New York, NY, 2018) of the Schrödinger Suite (Small-Molecule Drug Discovery Suite 2018-3, Schrödinger, LLC, New York, NY, 2018). This procedure was necessary to account for insertions and deletions present in the template structures (Supplementary Fig. 1). Structural modeling was also performed with the BioLuminate package using the energy-based model building method (Schrödinger Release 2018-3: Prime, Schrödinger, LLC, New York, NY, 2018). For identical residues in the alignment, side chain rotamers were retained, whereas for non-identical residues, side chain and main chain atoms were energy-minimized using the Prime module (Schrödinger Release 2018-3: Prime, Schrödinger, LLC, New York, NY, 2018) employing the VSGB solvation model46 and the OPLS3 force field47; all other settings were kept at their default values.
To generate atomic charges for tauro-CDC, we first generated a three-dimensional molecular structure of tauro-CDC in the Maestro interface (Schrödinger Release 2018-3: Maestro, Schrödinger, LLC, New York, NY, 2018) of the Schrödinger Suite. Further preparation of the structure in LigPrep (Schrödinger Release 2018-3: LigPrep, Schrödinger, LLC, New York, NY, 2018) (default settings) returned a single state with a negatively charged sulfonate moiety. Conformers of this structure were then generated in the MacroModel module (Schrödinger Release 2018-3: MacroModel, Schrödinger, LLC, New York, NY, 2018) using the Monte-Carlo Multiple Minimum search algorithm48, keeping all other settings at their default values. The conformer with the lowest potential energy that did not display intramolecular hydrogen bonding was subjected to quantum mechanical geometry optimization at the HF/6-31 G(d) level of theory in the GAUSSIAN 09 software (Revision A.02)49. A tight convergence criterion for the self-consistent field iteration process was set, and computation of electrostatic potential points with a density of ~1.68 pt/au2 (6 pt/Å2) was invoked. The geometry-optimized structure was visually inspected for the absence of intramolecular hydrogen bonds and subjected to the standard RESP procedure50,51 as implemented in the Antechamber set of programs to obtain the atomic point charges.
Binding modes for tauro-CDC in GluN2DLBD and GluN3BLBD were generated using the standard Induced Fit protocol implemented in the Schrödinger Suite25. The docking grid was centered on the coordinates of the bound ligand in the GluN2D and GluN3B template structure, respectively. In the initial Glide docking stage, the van der Waals radii of the receptor and ligand atoms were reduced to half their initial value, and a maximum of 20 poses were allowed to be carried over to the Prime (Schrödinger Release 2018-3: Prime, Schrödinger, LLC, New York, NY, 2018) refinement stage. For each generated pose, the receptor residues within 5 Å were energy-minimized and their side chain rotamers optimized. During the final Glide (Schrödinger Release 2018-3: Glide, Schrödinger, LLC, New York, NY, 2018)52,53 docking stage, tauro-CDC was redocked into all receptor conformers using XP precision54. The tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complexes with the lowest IFD score25 were considered for all subsequent calculations.
Molecular dynamics simulations of tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complexes
All molecular dynamics (MD) simulations were performed using the mixed single precision/fixed precision GPU (CUDA) version of PMEMD55 in the Amber14 suite of molecular simulation programs56. Hydrogen mass repartitioning57 was employed to enable a time step of 4 fs for integration. The Langevin thermostat58 with a collision frequency of 0.01 ps−1 and a target temperature of T = 300 K was used for temperature control. Covalent bonds involving hydrogen atoms were constrained using the SHAKE algorithm59. Long-range electrostatic interactions were estimated using the Particle Mesh Ewald method60, and a cutoff of 8 Å was used for short-range electrostatics and van der Waals forces.
All following steps were performed 10 times for each of the two complexes (tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD) so as to obtain 10 independent simulations per complex. The initial structures were minimized using a three-step procedure. First, the coordinates of all solute molecules were restrained by a harmonic potential with a force constant of 2.0 kcal mol−1 Å−2 while 2,000 steps of steepest descent minimization followed by 3,000 steps of conjugate gradient minimization were carried out. This step was repeated with the restraints switched from the solute to the solvent molecules. During the following final minimization step, the restraints were removed, and 3,000 steps of steepest descent minimization followed by 7,000 steps of conjugate gradient minimization were performed. 20 ps of NVT-MD (the solute was restrained with a force constant of 2.0 kcal mol−1 Å−2) were carried out while heating the system from 0 K to 300 K, followed by additional 5 ps of NVT-MD at 300 K. Density adaptation of the system was achieved by 75 ps of NPT-MD (solute restrained, force constant: 2.0 kcal mol−1 Å−2). An additional 1.7 ns of restrained NPT-MD were carried out before switching to the NVT ensemble. Here, 3.2 ns of restrained MD were performed prior to the start of the production phase, with harmonic restraints (force constant: 2 kcal mol−1 Å−2) applied to only those Cα atoms that are closest to the center of mass of a secondary structure element (α-helix or β-sheet). The subsequent production phase consisted of 500 ns of NVT-MD (restraints as in the final NVT step of the equilibration phase), resulting in an aggregate simulation time of 5 μs per complex (10 μs in total). Coordinates for analysis and post-processing were saved every 20 ps. Post-processing and analysis of the MD trajectories was performed in CPPTRAJ61 as implemented in AmberTools15. Trajectories were visually inspected with VMD62. The two-tailed Student’s t-test was used to determine statistically significant differences in time-averaged quantities between GluN2D and GluN3B.
Calculation of effective binding energies
Effective binding energies (ΔGeff) of tauro-CDC to GluN2DLBD and GluN3BLBD were calculated using the MM/PBSA and MM/GBSA approaches as implemented in the MMPBSA.py module63 in AmberTools1556. All calculations were performed on 500 snapshots per trajectory extracted at regular intervals of 1 ns, corresponding to a total of 5,000 snapshots per approach for both the tauro-CDC/GluN2DLBD complex and the tauro-CDC/GluN3BLBD complex. The MM/PBSA calculations were performed with values of 1 and 4 for the internal dielectric constant (εint), to test for robustness of the relative ΔGeff with respect to this parameter28. The polar part of the contribution to the solvation free energy was calculated by the linear Poisson-Boltzmann equation using an ionic strength of 100 mM and an external dielectric constant (εext) of 80. Solutions for the linear PB equation were computed with 1,000 iterations on a cubic grid with 0.5 Å spacing between grid points. The nonpolar part of the contribution to the solvation free energy was considered proportional to the solvent accessible surface area (SASA) and computed with the equation ΔGnonpol,solv = γ(SASA) + β, where γ and β are parameterized constants64. The SASA was calculated with a solvent probe radius of 1.4 Å, Tan & Luo radii65 for the protein, and mbondi radii66 for the ligands. The MM/GBSA calculations were performed using the modified OBC model (GBOBCII)67, an ionic strength of 100 mM and default values for γ (0.005 kcal mol−1 Å−2) and β (0.0 kcal mol−1).
Results are expressed as ΔGeff ± standard error of the mean (SEM), where ΔGeff is the average effective binding energy over all snapshots and the overall SEM is estimated as the SEM of the single trajectories propagated over all trajectories. The two-tailed Student’s t-test was used to determine statistically significant differences in ΔGeff between GluN2D and GluN3B.
Preparation of GluN1LBD/GluN2DLBD tetramer structures
The structure of the rat GluN1 LBD (GluN1LBD) was prepared analogously to the structure of GluN2DLBD (see above for further details), using the crystal structure of the rat GluN1 LBD (PDB ID: 1PB768) as a template to which only missing residues and loops were added during the modeling step. To construct the LBD tetramer from the individual LBD structures, the coordinates of the respective LBD monomers were superimposed onto their corresponding monomer units in the structure of the GluN1/GluN2D NMDA receptor (PDB ID: 5FXH69) (Fig. 10a).
Accelerated molecular dynamics simulation of the GluN1LBD/GluN2DLBD tetramer
A single, 500 ns long accelerated MD (aMD) simulation70 of the GluN1LBD/GluN2DLBD tetramer was prepared, heated, and equilibrated analogously to the classical MD simulations of the tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complex (see above). During the production phase, bias parameters of αD = 781.0 kcal mol−1 and αP = 50,035.0 kcal mol−1, a total dihedral energy threshold of EthreshD = 18,950.0 kcal mol−1, and a total potential energy threshold of EthreshP = −341,718.0 kcal mol−1 were set on the basis of empirical formulas that were previously used to estimate these parameters70,71.
Preparation of tauro-CDC//GluN1LBD/GluN2DLBD complex structures
To identify a possible allosteric binding site in the GluN1LBD/GluN2DLBD tetramer, the MDpocket software29 was applied on all 25,000 snapshots of the 500 ns long aMD trajectory (see above). A binding pocket at the GluN1/GluN2DLBD interface was identified into which tauro-CDC was docked, using the snapshot in which the selected pocket displayed the highest mean local hydrophobic density29,30 (Supplementary Fig. 2).
Molecular dynamics simulations of the tauro-CDC//GluN1LBD/GluN2DLBD complex
A single 500 ns long conventional MD simulation of the tauro-CDC//GluN1LBD/GluN2DLBD tetramer complex was generated and analyzed analogously to the classical MD simulations of the tauro-CDC/GluN2DLBD and tauro-CDC/GluN3BLBD complex (see above).
Supplementary information
Acknowledgements
The study was supported by the Deutsche Forschungsgemeinschaft SFB974, TP B05 to N.K. and financial support for GPU server to H.G. We thank Prof. Michael Hollmann (Ruhr-Universität Bochum, Germany) for iGluR cDNAs. H.G. is grateful to the Jülich Supercomputing Centre at the Forschungszentrum Jülich for computing time on the supercomputer JURECA and JUWELS (NIC project ID: HKF7 and HDD17) and to the “Zentrum für Informations- und Medientechnologie” (ZIM) at the Heinrich Heine University Düsseldorf for computational support.
Author Contributions
N.K. and H.G. designed the research, A.K. conceptualized and performed TEVC experiments, M.B. performed computations, all authors analyzed the data and contributed to manuscript writing. N.K. and H.G. acquired funding.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Angela Koch and Michele Bonus contributed equally.
Supplementary information
Supplementary information accompanies this paper at 10.1038/s41598-019-46496-y.
References
- 1.Mayer ML, Westbrook GL, Guthrie PB. Voltage-dependent block by Mg2+ of NMDA responses in spinal cord neurones. Nature. 1984;309:261–263. doi: 10.1038/309261a0. [DOI] [PubMed] [Google Scholar]
- 2.MacDermott AB, Mayer ML, Westbrook GL, Smith SJ, Barker JL. NMDA-receptor activation increases cytoplasmic calcium concentration in cultured spinal cord neurones. Nature. 1986;321:519–522. doi: 10.1038/321519a0. [DOI] [PubMed] [Google Scholar]
- 3.Kleckner NW, Dingledine R. Requirement for glycine in activation of NMDA-receptors expressed in Xenopus oocytes. Science. 1988;241:835–837. doi: 10.1126/science.2841759. [DOI] [PubMed] [Google Scholar]
- 4.Chatterton JE, et al. Excitatory glycine receptors containing the NR3 family of NMDA receptor subunits. Nature. 2002;415:793–798. doi: 10.1038/nature715. [DOI] [PubMed] [Google Scholar]
- 5.Hogan-Cann AD, Anderson CM. Physiological Roles of Non-Neuronal NMDA Receptors. Trends in pharmacological sciences. 2016;37:750–767. doi: 10.1016/j.tips.2016.05.012. [DOI] [PubMed] [Google Scholar]
- 6.Traynelis SF, et al. Glutamate receptor ion channels: structure, regulation, and function. Pharmacological Reviews. 2010;62:405–496. doi: 10.1124/pr.109.002451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Malayev A, Gibbs TT, Farb DH. Inhibition of the NMDA response by pregnenolone sulphate reveals subtype selective modulation of NMDA receptors by sulphated steroids. British journal of pharmacology. 2002;135:901–909. doi: 10.1038/sj.bjp.0704543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jang M-K, Mierke DF, Russek SJ, Farb DH. A steroid modulatory domain on NR2B controls N-methyl-D-aspartate receptor proton sensitivity. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:8198–8203. doi: 10.1073/pnas.0401838101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Horák M, Vlček K, Chodounská H, Vyklický L., Jr. Subtype-dependence of N-methyl-D-aspartate receptor modulation by pregnenolone sulfate. Neuroscience. 2006;137:93–102. doi: 10.1016/j.neuroscience.2005.08.058. [DOI] [PubMed] [Google Scholar]
- 10.Keitel V, et al. Expression and localization of hepatobiliary transport proteins in progressive familial intrahepatic cholestasis. Hepatology. 2005;41:1160–1172. doi: 10.1002/hep.20682. [DOI] [PubMed] [Google Scholar]
- 11.Glantz A, Marschall H-U, Mattsson L-Å. Intrahepatic cholestasis of pregnancy: Relationships between bile acid levels and fetal complication rates. Hepatology. 2004;40:467–474. doi: 10.1002/hep.20336. [DOI] [PubMed] [Google Scholar]
- 12.Makino I, Hashimoto H, Shinozaki K, Yoshino K, Nakagawa S. Sulfated and nonsulfated bile acids in urine, serum, and bile of patients with hepatobiliary diseases. Gastroenterology. 1975;68:545–553. [PubMed] [Google Scholar]
- 13.Schubring SR, Fleischer W, Lin J-S, Haas HL, Sergeeva OA. The bile steroid chenodeoxycholate is a potent antagonist at NMDA and GABA(A) receptors. Neuroscience Letters. 2012;506:322–326. doi: 10.1016/j.neulet.2011.11.036. [DOI] [PubMed] [Google Scholar]
- 14.Pilo de la Fuente B, Ruiz I, Lopez-de-Munain A, Jiménez-Escrig A. Cerebrotendinous xanthomatosis: neuropathological findings. J Neurol. 2008;255:839–842. doi: 10.1007/s00415-008-0729-6. [DOI] [PubMed] [Google Scholar]
- 15.Gómez-Vicente V, et al. Neuroprotective Effect of Tauroursodeoxycholic Acid on N-Methyl-D-Aspartate-Induced Retinal Ganglion Cell Degeneration. PloS one. 2015;10:e0137826. doi: 10.1371/journal.pone.0137826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hasanein P, et al. Modulation of cholestasis-induced antinociception in rats by two NMDA receptor antagonists: MK-801 and magnesium sulfate. European journal of pharmacology. 2007;554:123–127. doi: 10.1016/j.ejphar.2006.10.026. [DOI] [PubMed] [Google Scholar]
- 17.Dehpour AR, et al. Effect of NMDA receptor antagonist on naloxone-precipitated withdrawal signs in cholestatic mice. Hum Psychopharmacol. 2000;15:213–218. doi: 10.1002/(SICI)1099-1077(200004)15:3<213::AID-HUP159>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 18.Hosseini N, Nasehi M, Radahmadi M, Zarrindast M-R. Effects of CA1 glutamatergic systems upon memory impairments in cholestatic rats. Behavioural brain research. 2013;256:636–645. doi: 10.1016/j.bbr.2013.08.018. [DOI] [PubMed] [Google Scholar]
- 19.Hollmann M, et al. Zinc potentiates agonist-induced currents at certain splice variants of the NMDA receptor. Neuron. 1993;10:943–954. doi: 10.1016/0896-6273(93)90209-A. [DOI] [PubMed] [Google Scholar]
- 20.Erreger K, et al. Subunit-specific agonist activity at NR2A-, NR2B-, NR2C-, and NR2D-containing N-methyl-D-aspartate glutamate receptors. Molecular Pharmacology. 2007;72:907–920. doi: 10.1124/mol.107.037333. [DOI] [PubMed] [Google Scholar]
- 21.Chen PE, et al. Modulation of glycine potency in rat recombinant NMDA receptors containing chimeric NR2A/2D subunits expressed in Xenopus laevis oocytes. Journal of Physiology. 2008;586:227–245. doi: 10.1113/jphysiol.2007.143172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Awobuluyi M, et al. Subunit-specific roles of glycine-binding domains in activation of NR1/NR3 N-methyl-D-aspartate receptors. Molecular Pharmacology. 2007;71:112–122. doi: 10.1124/mol.106.030700. [DOI] [PubMed] [Google Scholar]
- 23.Schmidt A, et al. The bile acid-sensitive ion channel (BASIC) is activated by alterations of its membrane environment. PloS one. 2014;9:e111549. doi: 10.1371/journal.pone.0111549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Curras MC, Dingledine R. Selectivity of amino acid transmitters acting at N-methyl-D-aspartate and amino-3-hydroxy-5-methyl-4-isoxazolepropionate receptors. Molecular Pharmacology. 1992;41:520–526. [PubMed] [Google Scholar]
- 25.Sherman W, Day T, Jacobson MP, Friesner RA, Farid R. Novel procedure for modeling ligand/receptor induced fit effects. Journal of Medicinal Chemistry. 2006;49:534–553. doi: 10.1021/jm050540c. [DOI] [PubMed] [Google Scholar]
- 26.Kuzmanic A, Zagrovic B. Determination of ensemble-average pairwise root mean-square deviation from experimental B-factors. Biophysical Journal. 2010;98:861–871. doi: 10.1016/j.bpj.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Plattner N, Noé F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015;6:7653. doi: 10.1038/ncomms8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Homeyer N, Stoll F, Hillisch A, Gohlke H. Binding Free Energy Calculations for Lead Optimization: Assessment of Their Accuracy in an Industrial Drug Design Context. Journal of Chemical Theory and Computation. 2014;10:3331–3344. doi: 10.1021/ct5000296. [DOI] [PubMed] [Google Scholar]
- 29.Schmidtke P, Bidon-Chanal A, Luque FJ, Barril X. MDpocket: open-source cavity detection and characterization on molecular dynamics trajectories. Bioinformatics. 2011;27:3276–3285. doi: 10.1093/bioinformatics/btr550. [DOI] [PubMed] [Google Scholar]
- 30.Schmidtke P, Barril X. Understanding and predicting druggability. A high-throughput method for detection of drug binding sites. Journal of Medicinal Chemistry. 2010;53:5858–5867. doi: 10.1021/jm100574m. [DOI] [PubMed] [Google Scholar]
- 31.Yi F, et al. Structural Basis for Negative Allosteric Modulation of GluN2A-Containing NMDA Receptors. Neuron. 2016;91:1316–1329. doi: 10.1016/j.neuron.2016.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yao Y, Harrison CB, Freddolino PL, Schulten K, Mayer ML. Molecular mechanism of ligand recognition by NR3 subtype glutamate receptors. EMBO Journal. 2008;27:2158–2170. doi: 10.1038/emboj.2008.140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Richieri GV, Low PJ, Ogata RT, Kleinfeld AM. Mutants of rat intestinal fatty acid-binding protein illustrate the critical role played by enthalpy-entropy compensation in ligand binding. Journal of Biological Chemistry. 1997;272:16737–16740. doi: 10.1074/jbc.272.27.16737. [DOI] [PubMed] [Google Scholar]
- 34.Gertzen CGW, et al. Mutational mapping of the transmembrane binding site of the G-protein coupled receptor TGR5 and binding mode prediction of TGR5 agonists. Eur J Med Chem. 2015;104:57–72. doi: 10.1016/j.ejmech.2015.09.024. [DOI] [PubMed] [Google Scholar]
- 35.Hou T, Wang J, Li Y, Wang W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. Journal of Chemical Information and Modeling. 2011;51:69–82. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Genheden S, Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin Drug Discov. 2015;10:449–461. doi: 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gohlke H, Case DA. Converging free energy estimates: MM-PB(GB)SA studies on the protein-protein complex Ras-Raf. Journal of Computational Chemistry. 2004;25:238–250. doi: 10.1002/jcc.10379. [DOI] [PubMed] [Google Scholar]
- 38.Weis A, Katebzadeh K, Söderhjelm P, Nilsson I, Ryde U. Ligand affinities predicted with the MM/PBSA method: dependence on the simulation method and the force field. Journal of Medicinal Chemistry. 2006;49:6596–6606. doi: 10.1021/jm0608210. [DOI] [PubMed] [Google Scholar]
- 39.Mano N, et al. Presence of protein-bound unconjugated bile acids in the cytoplasmic fraction of rat brain. Journal of Lipid Research. 2004;45:295–300. doi: 10.1194/jlr.M300369-JLR200. [DOI] [PubMed] [Google Scholar]
- 40.Tripodi V, Contin M, Fernández MA, Lemberg A. Bile acids content in brain of common duct ligated rats. Ann Hepatol. 2012;11:930–934. doi: 10.1016/S1665-2681(19)31420-6. [DOI] [PubMed] [Google Scholar]
- 41.Gowert NS, et al. Defective Platelet Activation and Bleeding Complications upon Cholestasis in Mice. Cell. Physiol. Biochem. 2017;41:2133–2149. doi: 10.1159/000475566. [DOI] [PubMed] [Google Scholar]
- 42.Paoletti P, Bellone C, Zhou Q. NMDA receptor subunit diversity: impact on receptor properties, synaptic plasticity and disease. Nature Reviews Neuroscience. 2013;14:383–400. doi: 10.1038/nrn3504. [DOI] [PubMed] [Google Scholar]
- 43.Katoh, K., Rozewicki, J. & Yamada, K. D. MAFFT online service: multiple sequence alignment, interactive sequence choice and visualization. Brief Bioinform, 10.1093/bib/bbx108 (2017). [DOI] [PMC free article] [PubMed]
- 44.Ye Y, et al. GLProbs: Aligning Multiple Sequences Adaptively. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2015;12:67–78. doi: 10.1109/TCBB.2014.2316820. [DOI] [PubMed] [Google Scholar]
- 45.Vance KM, Simorowski N, Traynelis SF, Furukawa H. Ligand-specific deactivation time course of GluN1/GluN2D NMDA receptors. Nat. Commun. 2011;2:294. doi: 10.1038/ncomms1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Li J, et al. The VSGB 2.0 model: a next generation energy model for high resolution protein structure modeling. Proteins. 2011;79:2794–2812. doi: 10.1002/prot.23106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Harder E, et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. Journal of Chemical Theory and Computation. 2016;12:281–296. doi: 10.1021/acs.jctc.5b00864. [DOI] [PubMed] [Google Scholar]
- 48.Chang G, Guida WC, Still WC. An Internal Coordinate Monte-Carlo Method for Searching Conformational Space. J Am Chem Soc. 1989;111:4379–4386. doi: 10.1021/ja00194a035. [DOI] [Google Scholar]
- 49.Gaussian 09, Revision A.02 (Wallingford CT, 2009).
- 50.Bayly CI, Cieplak P, Cornell WD, Kollman PA. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J Phys Chem. 1993;97:10269–10280. doi: 10.1021/j100142a004. [DOI] [Google Scholar]
- 51.Wang J, Cieplak P, Kollman PA. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? Journal of Computational Chemistry. 2000;21:1049–1074. doi: 10.1002/1096-987X(200009)21:12<1049::AID-JCC3>3.0.CO;2-F. [DOI] [Google Scholar]
- 52.Friesner RA, et al. Glide: a new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. Journal of Medicinal Chemistry. 2004;47:1739–1749. doi: 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]
- 53.Halgren TA, et al. Glide: a new approach for rapid, accurate docking and scoring. 2. Enrichment factors in database screening. Journal of Medicinal Chemistry. 2004;47:1750–1759. doi: 10.1021/jm030644s. [DOI] [PubMed] [Google Scholar]
- 54.Friesner RA, et al. Extra precision glide: docking and scoring incorporating a model of hydrophobic enclosure for protein-ligand complexes. Journal of Medicinal Chemistry. 2006;49:6177–6196. doi: 10.1021/jm051256o. [DOI] [PubMed] [Google Scholar]
- 55.Le Grand S, Götz AW, Walker RC. SPFP: Speed without compromise-A mixed precision model for GPU accelerated molecular dynamics simulations. Comput Phys Commun. 2013;184:374–380. doi: 10.1016/j.cpc.2012.09.022. [DOI] [Google Scholar]
- 56.AMBER 14 (University of California, San Francisco, 2014).
- 57.Hopkins CW, Le Grand S, Walker RC, Roitberg A. Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. Journal of Chemical Theory and Computation. 2015;11:1864–1874. doi: 10.1021/ct5010406. [DOI] [PubMed] [Google Scholar]
- 58.Pastor RW, Brooks BR, Szabo A. An Analysis of the Accuracy of Langevin and Molecular-Dynamics Algorithms. Mol Phys. 1988;65:1409–1419. doi: 10.1080/00268978800101881. [DOI] [Google Scholar]
- 59.Ryckaert J-P, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics. 1977;23:327–341. doi: 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- 60.Darden TA, York DM, Pedersen L. Particle mesh Ewald - an N·Log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. doi: 10.1063/1.464397. [DOI] [Google Scholar]
- 61.Roe DR, Cheatham TE., III PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. Journal of Chemical Theory and Computation. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 62.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of molecular graphics. 1996;14(33-38):27–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 63.Miller BR, III, et al. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. Journal of Chemical Theory and Computation. 2012;8:3314–3321. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- 64.Sitkoff D, Sharp KA, Honig B. Accurate Calculation of Hydration Free-Energies Using Macroscopic Solvent Models. J Phys Chem. 1994;98:1978–1988. doi: 10.1021/j100058a043. [DOI] [Google Scholar]
- 65.Tan C, Yang L, Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. The Journal of Physical Chemistry B. 2006;110:18680–18687. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 66.Tsui V, Case DA. Theory and applications of the generalized Born solvation model in macromolecular simulations. Biopolymers. 2000;56:275–291. doi: 10.1002/1097-0282(2000)56:4<275::AID-BIP10024>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 67.Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 68.Furukawa H, Gouaux E. Mechanisms of activation, inhibition and specificity: crystal structures of the NMDA receptor NR1 ligand-binding core. EMBO Journal. 2003;22:2873–2885. doi: 10.1093/emboj/cdg303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Tajima N, et al. Activation of NMDA receptors and the mechanism of inhibition by ifenprodil. Nature. 2016;534:63–68. doi: 10.1038/nature17679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hamelberg D, Mongan J, McCammon JA. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J Chem Phys. 2004;120:11919–11929. doi: 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- 71.Pierce LCT, Salomon-Ferrer R, de Oliveira CAF, McCammon JA, Walker RC. Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics. Journal of Chemical Theory and Computation. 2012;8:2997–3002. doi: 10.1021/ct300284c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Scott, D. W. Multivariate density estimation: theory, practice, and visualization. 2. edn, (John Wiley & Sons, Inc., 2015).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.