Significance
Many cells travel within an organism to perform important duties in development, homeostasis, and disease. Questions remain as to why cells migrate in diverse forms: some travel as single cells, whereas others move collectively in groups of different sizes. What is also unclear is how extracellular conditions influence migration. In our study, which combines live imaging with theoretical modeling, we address these questions and reveal how both physical and chemical features of the microenvironment influence the optimum size of a migrating cell group.
Keywords: cell migration, theoretical modeling, three-dimensional, chemotaxis
Abstract
A long-standing question in collective cell migration has been what might be the relative advantage of forming a cluster over migrating individually. Does an increase in the size of a collectively migrating group of cells enable them to sample the chemical gradient over a greater distance because the difference between front and rear of a cluster would be greater than for single cells? We combined theoretical modeling with experiments to study collective migration of the border cells in-between nurse cells in the Drosophila egg chamber. We discovered that cluster size is positively correlated with migration speed, up to a particular point above which speed plummets. This may be due to the effect of viscous drag from surrounding nurse cells together with confinement of all of the cells within a stiff extracellular matrix. The model predicts no relationship between cluster size and velocity for cells moving on a flat surface, in contrast to movement within a 3D environment. Our analyses also suggest that the overall chemoattractant profile in the egg chamber is likely to be exponential, with the highest concentration in the oocyte. These findings provide insights into collective chemotaxis by combining theoretical modeling with experimentation.
The ability to sense and follow directional signals is essential for migrating cells. Gradients of chemical signals are believed to guide moving cells to their targets (1, 2). Classically, the formation of such a gradient involves a “source” that continuously produces a signal that freely diffuses through extracellular space and a “sink” that actively eliminates it (3–6). To study cellular responses, investigators have artificially created chemical gradients in vitro using gels (7, 8), micropipettes (9), and microfluidic devices (10–12). However, endogenous gradients are challenging to measure directly. Recently, endogenous promoter-driven fluorescence fusion proteins have been used to visualize a chemical gradient in vivo (13); however, such reporters usually give weak signals and the fluorescent tag can alter the molecule’s properties. Even when a signal can be detected, it reveals the bulk of the chemical, whereas the protein that is available for the migrating cell to sense may be a tiny, invisible fraction of the total (13). Moreover, in vivo, cells probably integrate information from multiple signals (6, 14), both biochemical and physical. Both the signal and the response may be quite different in 3D in vivo environments compared with 2D experimental paradigms. For all these reasons, it is important to analyze migrating cells in their native environments.
It is becoming increasingly apparent that, even though some cells migrate as individuals, many cells move in interconnected clusters, strands, or sheets (15). Clusters of cells are larger than individual cells and at least theoretically should be able to sample a chemical gradient over a greater distance, so that the difference between front and rear of a cluster would be more pronounced than for single cells. Thus, a large cluster of cells could in principle be more sensitive to weaker signals, more polarized, and thus migrate more effectively. However, existing experimental data from neural crest explants of different sizes showed that migration speed across a flat surface was unaffected by cluster size (16). In vivo, collectively migrating cells move through a 3D microenvironment, raising the possibility that a size–speed correlation, if it exists, might be missed in artificial cell culture environments. Moreover, if any size–speed correlation does exist, it remains to be seen whether it is positive or negative.
Theoretical modeling has been instrumental in probing basic questions in developmental biology for decades (17–19). It can reveal insights that are counterintuitive or difficult to ascertain experimentally. In this study, we combined live imaging of a simple and well-studied model of collective cell migration in the Drosophila ovary—the border cells—with theoretical modeling to investigate the chemical and physical features that influence their migration speed. We found experimentally, in vivo, a size–speed correlation that supports the theoretical prediction that larger clusters move faster in 3D but not on 2D surfaces. Moreover, our analysis suggests that the sum total of all chemoattractants that the border cells respond to, which includes at least four known ligands for receptor tyrosine kinases (RTKs), likely forms an exponential gradient. Finally, we report that the external physical constraints of the environment ultimately limit the increase in speed conferred by increasing cluster size. Thus, multiple features of the in vivo environment, both physical and chemical, exert effects on the speed and optimal size of a migrating group of cells.
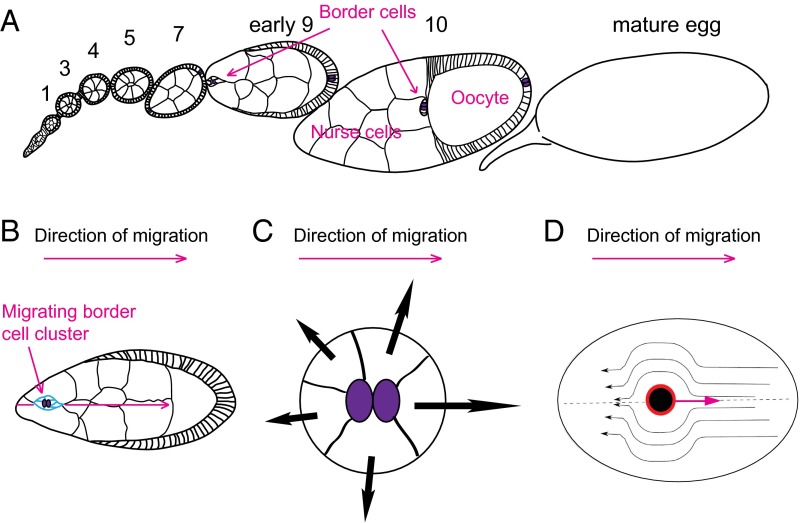
The Drosophila ovary is made up of 12–16 ovarioles, each of which serves as an “assembly line” of developing egg chambers (Fig. 1A). An egg chamber is composed of 16 germ cells surrounded by a single layer of somatic epithelial cells. A pair of specialized cells called polar cells develops at each end of each egg chamber and secretes Unpaired (Upd), a cytokine that activates JAK/STAT signaling in the surrounding epithelial follicle cells. At the anterior end, during developmental stage 9, these four to eight so-called border cells that receive high levels of JAK/STAT become migratory and carry the polar cells, which are not mobile, in-between the germ-line cells called nurse cells, until they reach the oocyte (20–22) (Fig. 1B and Movie S1). During migration, the cells respond to at least four secreted factors produced in the germ line: PDGF- and VEGF-related factor 1 (PVF1), which binds to and activates its receptor (PVR), as well as Spitz, Keren, and Gurken (Grk), which bind and activate epidermal growth factor receptor (EGFR), which like PVR is a receptor tyrosine kinase. Inhibiting both receptors in the border cells at the same time causes the cells to migrate poorly and sometimes off-track (23–26). It would be interesting to directly measure the spatial profiles of the ligands; however, antibodies are only available against PVF1 and Grk, and the extracellular protein is not abundant enough to detect. Therefore, we have no direct information about the shapes of the extracellular gradients or even if there are gradients at all.
Fig. 1.
Drosophila ovary and border cell migration simulations. (A) Drosophila ovariole containing egg chambers of increasing maturity. (B) Stage 9 egg chamber showing border cells at onset of migration. Border cells are in blue. (C) Schematic illustration of our model of chemotaxis of cellular clusters: due to the chemoattractant gradient, the cells at the cluster surface protrude and induce a force that is directed at the local outward normal, and is increasing with the local concentration of the chemical signal (black arrows). (A–C) Polar cells are in purple. (D) Schematic illustration of the drag sources on the border cell cluster (black circle) as it moves along the axis of the egg. One mechanism of drag is due to direct molecular binding with the surrounding cells (red rim of the cluster), and the second mechanism comes from the cytoplasmic flow around the cluster (streamlines with arrows).
Here, we developed a theoretical model that predicted that larger clusters would migrate faster than smaller ones in 3D but not in 2D. We then generated clusters of different sizes, both smaller and larger than those found in wild type (WT), and evaluated their migration speeds. Our results reveal that migration speed increases with increasing cluster size up to a point beyond which speed decreases precipitously. The drop in speed suggested that, in this confined 3D tissue, cluster speed is likely greatly affected by viscous drag and led us to refine the model. We also compared the observed changes in speed along the migration path to those predicted by simple mathematical models of responses to either linear or exponential gradients. Together, the combination of empirical observations and theoretical modeling emphasize the importance of analyzing cells in realistic microenvironments and show that both chemical and mechanical features influence the optimal size of a collectively migrating cluster in vivo.
Theoretical Model
During chemotaxis, cells migrate directionally in response to chemoattractants, moving up or down spatial gradients. However, because the functional chemoattractant molecules that are actually available to the migrating cell usually constitute only a small fraction of the total ligands, and multiple ligands may impinge simultaneously on a given cell or cell group, the shape of chemoattractant gradient seen by the cell, in most systems is unknown. In the border cell system, PVF1 and three ligands for the EGF receptor—Spitz, Keren, and Gurken—may form either exponential or linear gradients, or some combination, to guide border cell migration. An exponential profile would most likely form by continuous ligand secretion by the oocyte and concomitant removal of ligands by surrounding follicle cells, all of which also express PVR and EGFR.
To model border cell migration, we assume for simplicity that each cluster has a spherical shape, whose surface is made up of a single layer of border cells. Each cell at the cluster surface produces a pulling force that points along the outward normal to the sphere, and is an increasing function of the local concentration (c) of the chemoattractant (Fig. 1C). This pulling force is exerted by the border cells on the surrounding nurse cells, through the extension of lamellipodia and filopodia, which adhere to the surrounding matrix and then contract, thereby pulling the border cells forward. The relation is linear for low concentrations, whereas at high concentrations we expect this relationship to saturate at a maximal cellular pulling force. The force per unit area of cell membrane in contact with the chemoattractant, depends on the response function S(c), which is the fraction of activated receptors at the cell surface, and for a simple process (Supporting Information, Eqs. S1–S6, and see Table S1 for full list of variables and parameters used in the model), we get as follows:
| [1] |
where represents the ratio between the affinity of the chemoattractant to the receptors, and the endocytosis rate, assuming the chemoattractant to have a gradient only along the x direction. The simplest relation between the local pulling force that is triggered at the border cell surface, and the local level of activated receptors to the chemical signal, is a linear relation of the following form:
| [2] |
is a proportionality factor. We will assume this simple relation in the following model, and note that any monotonic relation will give the same qualitative results. Integrating the x component of the forces along the surface for a spherical cluster located at a certain position 0 ≤ x0 ≤ L, we get the resultant total chemotactic force up the gradient:
| [3] |
For a linear concentration profile, c(x) = c0 + x (cm − c0)/L, we get the following:
| [4] |
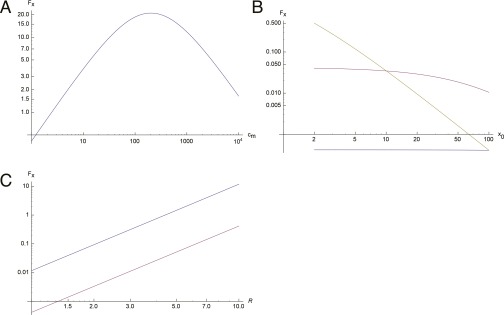
where c0 and cm are the concentrations at x = 0 and x = L, respectively. The behavior of the force for a linear profile, according to Eq. 4, is shown in Fig. S1. As a function of the chemical gradient () (Fig. S1A), we see that the force initially increases for weak gradients, but then decreases for large gradients due to the saturation of the response S(x) (Eq. 1). The force monotonously decreases with cluster position up the chemical gradient (Fig. S1B), and increases with cluster size as follows: ∝ R3 (Fig. S1C).
Table S1.
List of variables
| Variable | Meaning |
| S (x) | Response function (fraction of activated receptors on the surface of border cell cluster) |
| Ratio between affinity of the chemoattractant to the receptors, and the endocytosis rate | |
| c (x) | Local concentration of the chemoattractant |
| A | Proportionality factor |
| Local pulling force | |
| Total force along x direction | |
| R | Border cell cluster radius |
| Regg | Egg chamber radius |
| L | Length of total migration path |
| D | Diffusion coefficient |
| Length scale of the exponential profile decay | |
| γ | Rate of ligand removal |
| Friction coefficient of the cluster | |
| Coefficient of confined viscous drag | |
| Velocity | |
| τ | Persistence time |
| Probability | |
| Number of border cells at cluster surface | |
| Constant |
Fig. S1.
Behavior of the resultant force (Eq. 4) for a linear chemical profile. The y axes are force in log scale. (A) As a function of the maximal concentration cm. We find a linear increase of the force for shallow gradients, and a saturation-driven slowing down for steep gradients [calculated at a fixed position ()]. (B) Force as a function of the position along the gradient () for three values of the gradient () (blue, purple, and yellow indicate increasing values of ). (C) ∝ R3 behavior.
This force (Eq. 4) can be approximated by a simpler expression, for example by expanding Eq. 4 for large as follows:
| [5] |
or for small as follows:
| [6] |
Both these simplified expressions (Eqs. 5 and 6) allow to clearly identify the ∝ R3 scaling of the size dependence of the force. This scaling relation has a simple intuitive origin: the cluster area where pulling force is being exerted increases as R2, whereas the difference in the opposing forces between the front and back due to the chemical gradient increases as R, resulting in the cubic power law.
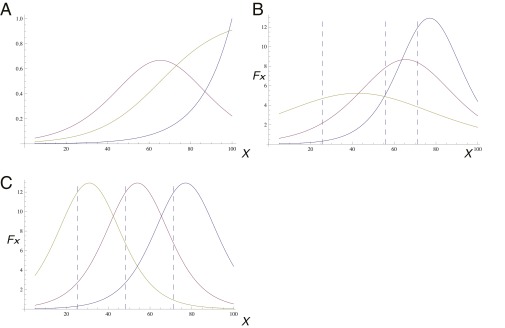
An exponential concentration profile has the following form: , where is the length scale of the exponential profile decay, D is the diffusion coefficient of the secreted factor, and γ is its rate of removal. The resulting expression for the total force is given in Supporting Information (Eq. S9), and similarly to the linear profile we get that the total force increases as ∝ R3. The intriguing feature is that the total force now has a nonmonotonous dependence on the position, with a distinct peak at the inflection point of the signaling function S(x) (Fig. S2 A–C). The reason for this peak is that the local response function of the cells to the chemical (Eq. 1) has an inflection point along an exponential profile, where it has its maximal spatial gradient. This maximal gradient translates into a maximal difference between the pulling forces at the front and back of the cluster, giving a maximum in the total force.
Fig. S2.
(A) Calculated velocity (purple line, from Eq. S9) of a cluster moving up an exponential chemical gradient (blue line). The response function S(x) is shown by the yellow line, and we see that the peak in the cluster velocity corresponds to the steepest part of the response (using: c0 = 0, cm = 10, = 1, ξ = 15, R = 5, L = 100). The values are normalized for comparison. (B) The total force (proportional to cluster velocity) of the cluster up the exponential gradient, from Eq. S9 (using c0 = 0, cm = 10, = 1, R = 5, L = 100), for different values of ξ = 25, 15, 10 (Left to Right). (C) As in B (using: c0 = 0, cm = 10, ξ = 10, R = 5, L = 100), for different values of = 1, 10, 100 (Right to Left). In B and C, the approximate locations of the peak in the cluster velocity, according to xpeak (Eq. S10), are denoted by the vertical dashed lines.
The center-of-mass velocity of the cluster is determined by the following Langevin equation (in the limit of vanishing inertia), where the effective friction force balances the pulling forces:
| [7] |
where is the friction coefficient of the cluster and is the sum of the random pulling forces due to cellular noise. The mean directed velocity is simply given by the following:
| [8] |
The friction coefficient has two contributions (Fig. 1D): (i) Molecular contacts between the moving cluster and the surrounding cells, in the form of transient adhesions, give an effective friction that is simply proportional to the cluster surface area: λad ∝ R2. (ii) Viscous flow of the cytoplasm of the surrounding nurse cells gives rise to a drag as for a sphere moving through a viscous fluid, i.e., Stokes’ law: λvis ∝ R.
The total drag is the combination of these two dissipation mechanisms, so that we have the following: λ = λad + λvisc. Due to the finite lateral confinement of the hard wall of the egg chamber, the viscous drag increases above the simple Stokes’ law when the ratio R/Regg approaches unity. This effect is usually described in terms of a polynomial expansion of this ratio (27):
| [9] |
The coefficients can be either positive or negative. For a single power i, and a positive , we now get that the drag force tends to diverge as the ratio increases in magnitude and approaches unity. For simplicity, we use here only one value of power i, and = 1.
Note that our system is different from the scenario of a 2D, in vitro layer of cells where the viscous drag from the infinite overlying buffer is indeed negligible compared with the effective contact friction with the substrate (28). In the confined 3D volume of the egg, it is not clear a priori whether the viscous contribution is important, which is why we write the model in a general form containing both friction contributions. It turns out (see below) that the observed scaling strongly supports the conclusion that the drag from viscous flow is dominant in this system.
From Eqs. 3 and 8, we see that the average velocity in the direction of the chemical gradient increases with the cluster radius: linearly when surface contacts dominate ⇒ ∝ R, and quadratically when viscous drag dominates ⇒ ∝ R2. Larger clusters move at a higher velocity in a chemical gradient, due to their ability to sense the gradient over a larger length scale. Note that we disregard internal motions and dissipation due to friction forces between the cells of the cluster, because we are interested in the cluster motion as a whole, and recent data suggest that the cluster behaves as a multicellular unit (29). Such motions are observed to be small, as the border cells strongly adhere to the core polar cells (29).
We next want to compute the velocity fluctuations of the clusters. The data on the fluctuations of the cluster velocity in the direction orthogonal to the chemical gradient (y), so presumably unaffected by it, indicate a rather constant background noise level that is inherent to the cluster motion. This noise may be described as an additive noise source, inherent to the pulling forces that each cell at the cluster surface produces. There are two limiting cases in which the random forces induced by each cell are (i) uncorrelated or (ii) correlated with its neighbors. Cell–cell correlations are evident in collective cellular motion (30, 31). We will characterize the random active forces induced by the individual cells as having a typical force f0, a mean burst duration τnoise (persistence time of the cellular pulling force), and mean waiting time between bursts τ. We then solve the Langevin equation for the center-of-mass motion of a cluster (32), in the limit of vanishing inertial effects λτnoise ≫ 1. We therefore get the following:
| [10] |
| [11] |
where = τnoise/(τ + τnoise) is the probability for the random cellular force to be active, and we give the case of uncorrelated (Eq. 10) and perfectly correlated (Eq. 11) noise. The number of cells at the cluster surface ∝ R2.
From the previous section, we found that the drag has two contributions: For contact dominated friction λ = λ0Ns ∝ R2, we get the following:
| [12] |
| [13] |
whereas for viscous-dominated drag, , we get the following:
| [14] |
| [15] |
We therefore find that uncorrelated pulling noise can result in reduced sideways meandering of larger clusters (Eq. 12), whereas correlated noise may even cause it to increase (Eq. 15). However, uncorrelated (correlated) noise for viscous-dominated (contact-dominated) friction predicts the sideways motion to be size independent (Eqs. 13 and 14).
Results
Dependence of Speed on Cluster Size.
We predict that the resultant pulling force due to the chemical gradient (, Eq. 3) is proportional to R3 for a cluster migrating in a 3D environment, whereas this force would be proportional to R2 for a cluster migrating on a 2D surface such as a coverslip (Supporting Information) (33). Because the friction coefficient (λ) in 3D scales as either R2 or R, the cluster velocity, which is inversely proportional to λ, should increase with increasing cluster diameter in 3D (Eq. 8). Whereas in 2D, the friction is dominated by the surface area, therefore λ scales as R2 and we expect the velocity to be independent of the cluster diameter (33).
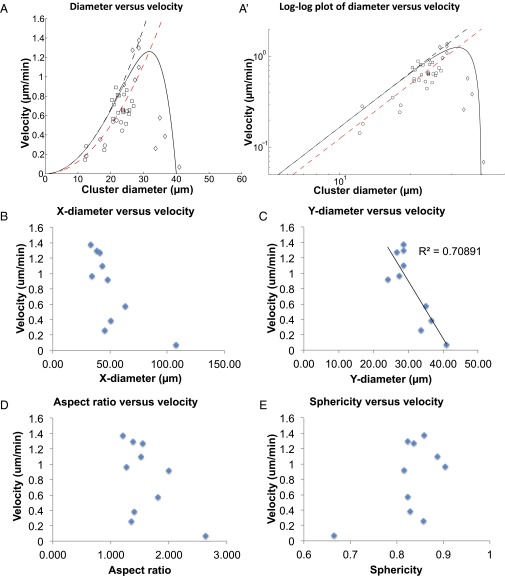
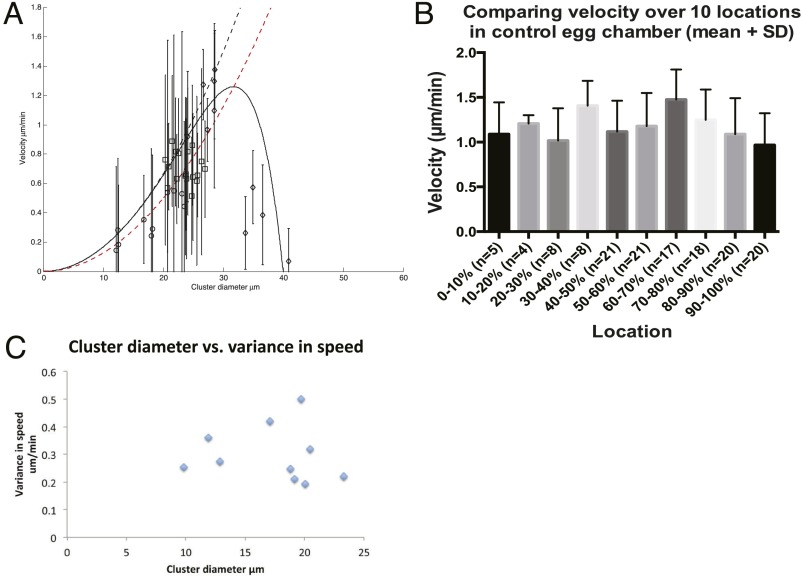
To test the prediction that migration speed is positively correlated with cluster size in a 3D environment, we measured the average diameter and average speed of border cell cluster in each movie, and plotted diameter–speed data from 18 different WT movies (Fig. 2A, square). To obtain even smaller clusters, we knocked down E-cadherin specifically in central nonmotile polar cells, which causes clusters to break apart (29). Compared with other methods that generate smaller border cell clusters (34, 35), this method does not directly alter the migrating cells themselves, thus presumably minimally changing their properties, and the smaller clusters generated are able to migrate. We measured average speed and average cluster size from 10 UpdGal4, UAS-EcadRNAi movies (Fig. 2A, circles), and combined them with 18 WT movies (Fig. 2A, squares). Our data revealed that cluster speed increases up to a diameter of 24 µm (R = 12 µm), beyond which the velocity saturates (Fig. 2A). The increase of speed with size is found to be consistent with the predicted quadratic behavior, thereby indicating that the dominant mode of friction is most likely due to the viscous (Stokes) flow of the nurse cells’ cytoplasm around the cluster.
Fig. 2.
Dependence of mean cluster velocity on the cluster radius. (A) Symbols show data points averaged from different experiments: Circles, E-cadherin k.d. (UpdGal4, UAS-EcadRNAi); squares, WT; diamonds, mutant extralarge clusters. Solid black line gives the fit to Eq. 16, using , i = 6, Regg = 20 μm, β = 150 (μm⋅min). Dashed black line, , such that the effects of the confining shell are ignored. The red dashed line denotes the fit to the WT and E-cadherin k.d. data using these parameters: Regg = 26 μm, β = 200 (μm⋅min). A′ shows a log–log plot to highlight the power-law behavior of small clusters, , which indicates the dominant role of viscous drag. (B–E) Plotting x-axis diameter (B), y-axis diameter (C), aspect ratio (D), and sphericity (E) against velocity. Lines of linear regression were shown and R2 were indicated in C.
The data also had an indication that the velocity saturates for the largest clusters in this dataset. This led us to reason that due to the confinement of the rigid extracellular matrix (ECM), if the clusters increase further in size they approach the limit of a “plug” where the flow around the cluster is highly inhibited (Fig. 1D), and the motion is blocked. This phenomenon is described by the following general expression that combines the two drag mechanisms (Eqs. 8 and 9):
| [16] |
where α and β give the relative weight of the two drag mechanisms, and Regg is the effective radius of the rigid confinement of the viscous flow (i is a fit parameter, usually larger than 1). The fit of Eq. 16 to the WT and E-Cadherin knock-down (k.d.) data (Fig. 2A, solid curve) indicates that molecular contacts (α) play a small role, and that viscous drag (β) is the more important determinant of border cell migration speed. We next exploited a number of mutations that cause extra polar cells to form, resulting in recruitment of extra border cells and larger border cell cluster size (36, 37) (Movie S2). This allowed us to determine how migration speed correlates with larger-than-normal cluster size. Strikingly, in large clusters, velocity plummets with increasing cluster diameter (Fig. 2 A, diamond, and C), just as we expected for confined viscous flow (Eq. 16). This is in stark contrast to the prediction that cluster speed should increase uniformly with cluster size (Fig. 2A, dashed curves), suggesting that, in this 3D microenvironment, due to the physical confinement of the egg chamber by a stiff ECM, viscous drag force is larger than in an infinite medium. This is in contrast to 2D where viscosity of the fluid medium covering cells is not important (28).
Border cells move in a confined space delineated by nurse cells and the surrounding ECM. Moreover, the huge nurse cell nuclei further decrease the effective radius of the rigid confinement Regg, such that it is much smaller than the radius of the actual egg chamber (which is ∼50–100 µm depending on the position within the egg chamber). When the border cell cluster is small (i.e., diameter ≤ 24 µm), the ability to sample a larger distance within chemical gradient causes faster migration for larger clusters. However, as the cluster becomes larger (i.e., diameter > 24 µm), the confinement of the viscous flows in the surrounding nurse cells increases sharply. Therefore, further increases in cluster size have a negative impact on speed (Movie S2). Note that extra large border cell clusters tend to be more elongated than WT and polar cell Ecad k.d. clusters. However, average velocity does not correlate strongly with shape (Fig. 2 D and E). We used y-axis diameter in calculations because x-diameter elongation could be affected by thin extensions of cells between the surrounding nurse cells, and these extensions do not conform to the treatment of drag arising from bulk viscous flow. Indeed, for extralarge clusters, y-axis diameter (Fig. 2C) correlates better than x-axis diameter (Fig. 2B) with average cluster velocity.
Fluctuation in Migration Speed.
The model predicts that, if the individual noise in the cells’ pulling forces is uncorrelated, and friction is dominated by cluster surface contacts, then the velocity variance in the direction perpendicular to the chemical gradient should decrease as follows: (Eq. 12). However, if viscous drag from the surrounding nurse cells dominates, then (Eq. 14). From our experiments, we compared the total variance in the direction perpendicular to the chemical gradient in clusters of different sizes, generated by polar cell-specific E-cadherin k.d. We find that the variance, which is the root-mean-square does not vary with R, and stays approximately at the same level (Fig. S3C), again indicating that friction from viscous drag dominates during border cell migration.
Fig. S3.
(A) Dependence of mean cluster velocity on cluster radius, with SD shown. (B) Cluster velocity in relation to cluster position along the migration path. (C) Variance in the y-direction velocity as a function of the cluster diameter. Symbols are data points averaged from individual experiments.
Shape of the Chemoattractant Gradient.
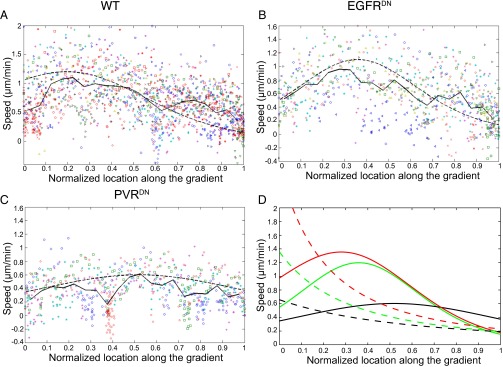
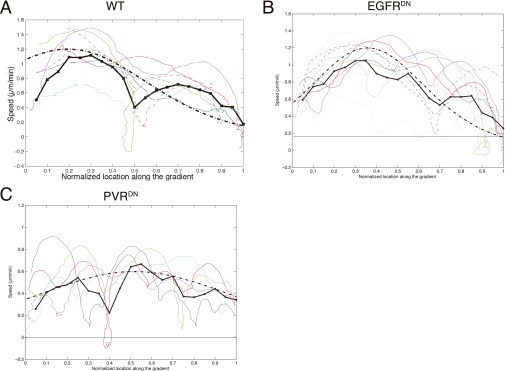
To understand whether the overall chemical gradient in the egg chamber is linear or exponential, we extracted migration speed data from WT border cell migration movies, and plotted speed against distance traveled, expressed as a fraction of the total migration path (Fig. 3A and Fig. S4). Averaging 20 different WT movies, we obtained a percentage migration speed line shown in solid line. Each individual movie shows decrease of cluster migration speed to around zero at the end of migration, consistent with our hypothesis that, as border cells migrate up the chemical gradient, their guidance receptors saturate, causing them to lose front–back polarity. However, instead of a steady decrease in speed, border cells accelerate first after they start migrating, and then decelerate as they move toward the oocyte, an effect that resembles the theoretical response to an exponential chemoattractant gradient model, as shown in the dashed line (Fig. 3A). This initial increase in speed does not result from border cells escaping from the anterior end of the egg chamber, because in the majority of movies where the acceleration occurred at the onset of migration, detachment from the anterior end had already taken place before the acceleration (Fig. S5C). Therefore, the overall chemoattractant gradient likely increases exponentially with highest concentration at the oocyte. We also plot a fit to the motion in a linear chemical profile (Fig. 3D, red dashed line), which monotonously decreases and does not reproduce the peak in velocity observed at 20–30% of the trajectory. However, the noise in the measured motion, and in particular the large oscillations in the motion due to several slow phases (“pauses”) (Fig. 3 and Fig. S4), does not allow us to definitely discriminate between the exponential and linear profiles.
Fig. 3.
Migration profiles of WT and receptor-deficient clusters. Migration speeds at different positions along migration path in WT (A), slboGal4; EGFRDN (B), and slboGal4; PVRDN (C) egg chambers. Symbols of same color and shape indicate data points from the same movie. Solid lines give the average of all of the experiments. Dashed line gives the fit to Eq. 17. (D) Theoretical fits to WT (red), EGFRDN (green), and PVRDN (black) migration speed using exponential (solid lines) and linear (dashed lines) chemoattractant concentration profile.
Fig. S4.
Velocity up the gradient, for several experiments. Colored lines are individual WT (A), EGFRDN (B), and PVRDN (C) experiments, averaged every five time points for smoothening. The thick black line gives the average of all of the experiments, and the thick dashed-dot black line gives the fit to Eq. 17. The peak value of the theoretical expression is normalized to velocity of 1.2 µm/min.
Fig. S5.
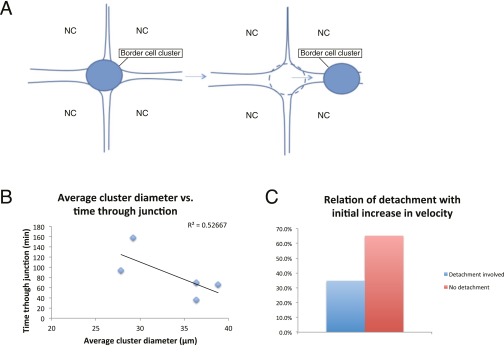
Nurse cell influence on border cell migration. (A) Illustration of border cell cluster untrapping from a nurse cell–nurse cell junction. NC, nurse cell. (B) Time spent untrapping from a junction in relation to cluster size. Linear regression was done and linear plot was shown in the graph. (C) Percentage of border cell migration movies that show an initial increase in speed that have detachment (blue bar) and no detachment (red bar) involved.
We next want to understand the relative contributions of different ligands to the overall chemoattractant profile. The migrating border cells express both PVR and EGFR. We expressed a dominant-negative (DN) form of EGFR (EGFRDN) (24) in border cells, so that they can only respond to PVF1 ligand. We plotted speed vs. percentage of migration from 10 different experiments and averaged all of the experimental data (solid line in Fig. 3B). A dashed black line gives the model calculation using an exponential gradient with these parameters: = 0, = 40, ξ/L = 0.17. The peak value of the theoretical expression is normalized to a velocity of 1.2 μm/min (using A/λ = 6.4). We see that, although individual traces have oscillations in the velocity, the average is rather smooth, with a maximum of the velocity located at about ∼35% of the trajectory. As for the WT, the noise level and the repeated pauses do not allow us to definitely rule out also a linear profile (Fig. 3D, green dashed line). However, because the exponential profile seems to allow for a better fit, we use it in the analysis. In the absence of EGFR signaling, the velocity profile looks similar to that of WT, with an initial increase in speed followed by decrease as the cluster approaches the oocyte. This indicates that Pvf1 forms an exponential gradient along border cell migration path, and is sufficient alone to guide border cell migration to the oocyte. This is consistent with previous results (24). On the other hand, expressing PVRDN specifically in the border cells limits the ability of cells to migrate, indicating that EGF ligands Spitz, Keren, and Gurken are not fully sufficient for chemotaxis of border cells toward the oocyte. The velocity is almost a constant, with a very weak peak at around ∼50% of the trajectory (Fig. 3C). To fit the data, we used the following: = 0, = 5, ξ/L = 0.3, and A/λ = 7.2, indicating that the EGFR ligands produce a combined signal that suggests lower affinity of binding and thus of uptake, and so a lower rate of removal. Together, this results in the form of an exponential gradient with a much longer decay length. The WT behavior (Fig. 3A), combining both signals, is described most simply by adding the two processes as triggering the overall motility response of the cells:
| [17] |
using the affinity parameters fitted for the isolated signals, and A/λ = 4.6. The noticeable feature is that, due to the combined effect of both factors, in WT (Fig. 3A) the peak velocity is achieved earlier compared with Pvf1 alone (Fig. 3B), at 20–30% of the trajectory.
Discussion
Border cell migration in the Drosophila ovary has been an excellent model to study collective cell migration in a native, 3D environment. Having identified appropriate culture and imaging techniques, we are now able to capture the entire 4- to 6-h process live and obtain a wealth of data. In this paper, we combined theoretical modeling with experimental measurements to answer an important question in the field of collective cell migration: which features of the microenvironment influence the speed and optimal size of a collectively migrating group of cells?
In this study, we discovered a correlation between size and speed of migrating clusters to address a long-standing question. Does the increase in size in collectively migrating cells help them sense the gradient better and achieve more efficient migration? A recent study of Xenopus neural crest cells reported no size–speed correlation in migrating explants observed in 2D culture (16). In contrast, we find that size matters for migrating border cell clusters. One possible explanation for the discrepancy is that the neural crest cells were analyzed as they moved on a 2D surface, although their normal migration occurs in a 3D environment. We analyzed border cell migration in their natural 3D environment as they move in-between nurse cells. Our model predicts just this difference between 2D and 3D. Other studies have reported key differences between cellular behaviors and molecular mechanisms in 2D vs. 3D (38). It will be interesting to determine whether, in other 3D chemotactic cell migration models, larger clusters move faster as predicted by our model. Another study recently undertook a more complex model of border cell migration, which also predicted increasing speed with increasing size within the normal range of four to eight cells (39). It is interesting that these complex simulations predict qualitatively the same behavior as our simple and thus analytically tractable model. This makes our experimental validation of the predictions satisfying. We go even further to predict, and then to show, that this relationship only holds for a particular range of cluster sizes.
The benefits of increasing cluster size do not increase without limit. For border cells, speed increases until cluster reaches 24 µm. Further increase in cluster size leads to a precipitous decrease in speed, attributable to stronger viscous drag due to confinement by the surrounding nurse cells. Potential caveats exist because we assume that the border cell cluster is a perfect sphere. The influence of viscous drag could be reduced for larger clusters if they become elongated rather than spheroid. This may explain the observed elongated morphology of, for example, the zebrafish lateral line primordium (40). Another solution to reducing the influence of viscous drag was recently described for cranial neural crest cells, which migrate collectively as a large group. Instead of splitting into small clusters, these cells reduce the strength of cell–cell adhesions so that they can move in a more fluid-like manner (41). Note that we find that chemotactic migration in 3D mimics the kinematic behavior of objects falling under gravity or bubbles rising through a confined column of viscous medium. Although the sources of the forces are different, the resulting behavior is strikingly similar.
We also used the measured speed along the migration path to deduce that the overall chemoattractant profile in the egg chamber is more likely to be exponential, with highest concentration in the oocyte, than linear. This is difficult to measure directly because (i) antibodies only reveal the bulk of the chemical, whereas the protein that is available for the migrating cell to sense may be a tiny, invisible fraction of the total; and (ii) border cells integrate responses to multiple chemical signals. Moreover, experimental manipulation using PVRDN and EGFRDN lines reveals the relative contributions of PVR and EGFR ligands to the overall chemical profile: PVF1 forms a sharp exponential gradient, whereas EGFR ligands Gurken, Keren, and Spitz exhibit a shallower exponential with a much longer decay length. One interpretation of these data is that they interact with lower affinity and thus are removed more slowly.
Other studies have compared linear vs. exponential chemoattractant gradients in cell migration. For example, using microfluidic devices, Herzmark et al. (42) generated linear and exponential f-Met-Leu-Phe (fMLP) gradients and watched the chemotactic responses of neutrophil-differentiated HL60 cells in these gradients. Similar to our modeling, they concluded that HL60 cells chemotax best at the low end of a linear concentration gradient, whereas in an exponential gradient, HL60 cells show highest chemotactic migration velocity in the middle of migration (42). However, it remains uncertain what chemoattractant profiles cells encounter in vivo. Our finding here in the Drosophila border cell migration system is an in vivo example that suggests the existence of multiple exponential chemoattractant gradients.
Our results raise the question as to why the sizes of WT clusters are poised close to the highest migration velocities (Fig. 2A). We wonder if there is an advantage to rapid movement. The complete process of oogenesis requires several days so it is not immediately clear why border cell migration speed would need to be optimized. However, migrating border cell clusters encounter nurse cell junctions along the migration path, and can get trapped in those junctions (see the dips in migration speed in Fig. S4). A simple analysis of the forces in such junctions (Supporting Information) suggests that it is necessary for a migrating cluster to achieve certain size so that chemotactic forces are able to overcome the osmotic pressure from nurse cells, and pull the cluster out of nurse cell junctions (Fig. S5). Indeed, we see that, when a border cell cluster gets larger, it takes less time to escape nurse cell junctions (Fig. S5). Evolutionarily, this might be another reason that larger cluster size is selected and suggests that multiple physical constraints of a tissue exert powerful influences on optimal cluster size and migration speed.
Examples of collective cell migrations abound in normal development, in tissue homeostasis, and in diseases, most notably cancer (reviewed in ref. 43). Collective migration may be the rule rather than the exception in metastasis, despite the physical challenges posed by squeezing groups of cells into blood and lymphatic vessels (44). Additional examples of collective migrations include blood vessel sprouting, epithelial closures, and innumerable embryonic morphogenetic movements. Cells move in groups of diverse sizes and varying arrangements through equally complex microenvironments. The border cells represent a clear example of how collective movement can enhance direction sensing (29) and how the combined chemical and physical properties of the microenvironment influences the optimal cluster size. The results presented here therefore lead us to propose that the details of the diverse physical and chemical microenvironments likely exert a strong influence on the observed sizes and arrangements of collectively migrating cells in vivo.
Materials and Methods
Fly Stocks and Egg Chamber Live Imaging.
SlboGal4, UAS-dsRedNLS; UAS-moesinGFP, and slbo-Lifeact-GFP flies were used for live imaging and were described before (26, 29). UAS-PVRDN, UAS-EGFRDN, and UAS-EcadRNAi (VDRC: KK103962) were described previously (23, 24, 26, 29). Fly fattening, dissection, and live imaging follow the established protocol (45).
Theoretical Modeling.
Please see Supporting Information for the details of theoretical modeling.
Registration of Egg Chambers.
To correct for egg chamber movement and/or growth during imaging, we measured border cell speed relative to the center of egg chamber by registering the outlines from frame to frame. We first used StackReg plugin (rigid body) in Fiji [ImageJ 1.49c; National Institutes of Health (46)] to align the egg chambers. Then we designed a Matlab code to further align the egg chambers (Supporting Information).
SI Theoretical Modeling
Calculated Response to the External Signal: Constant Receptor Recycling Rate.
Consider membrane receptors that are in an empty form (ρn), and those that got attached to the signaling molecule (ρa). We consider endocytic activity that removes both receptors indiscriminately, with constant rate Γ.
The equations of motion are as follows:
| [S1] |
where c is the local concentration of the signal molecule.
| [S2] |
where α is the rate at which new receptors are brought to the membrane. Solving Eq. S1, we get at steady state:
| [S3] |
Solving Eq. S2, we get at steady state:
| [S4] |
Using these solutions, we find that the steady-state concentration of activated receptors is as follows:
| [S5] |
Conservation of the total number of receptors gives ρn + ρa = 1, and together with Eq. S3, we find that α = Γ, so that the density of activated receptors is as follows:
| [S6] |
which is Eq. 1 with , because the local signal is proportional to density of activated receptors: S ∝ ρa.
Exponential Concentration Profile.
First, how does an exponential concentration gradient arise naturally in the organism? When a chemical is produced at one end of a (roughly) 1D object, and then diffuses from that source (with diffusion coefficient D) while being degraded at a constant-rate γ everywhere, we end up with the following exponential concentration profile:
| [S7] |
where cm is the maximal concentration at the source (located at x = L). We can generalize this profile, by adding the possibility of some constant background concentration c0:
| [S8] |
Using this concentration profile in Eqs. 1–3, we get for the mean force up the chemical gradient the following complicated expression:
| [S9] |
where is the length scale of the exponential profile decay, and Li2(z) is the poly-logarithm function. The intriguing feature of the velocity up the exponential gradient is that there is now a nonmonotonous dependence on the position, with a distinct peak of the velocity at the inflection point of the signaling function S(x) (Eq. 1), as shown in Fig. S2A.
Let us explore the behavior of the velocity in the exponential gradient. For the location of the peak, we can find an approximate expression:
| [S10] |
In Fig. S2B, we plot the velocity up the exponential gradient for several values of ξ. We find that with increasing ξ the exponential decay is spread over a longer length, and so the peak is shifted away from the source. Because the gradients of the concentration profile are smaller, the value at the peak is also lower. The agreement between the location of the peak and the approximate expression Eq. S10 is reasonable (consistently shifted to lower values), giving the correct trend.
Similarly, we show the effect of changing the value of the parameter ε in Fig. S2C.
Cluster Untrapping While Migrating In-Between Nurse Cells.
Migrating border cells frequently (two to approximately three junctions per entire migration) encounter nurse cell–nurse cell junctions that can slow down the migration and trap border cells for several minutes up to an hour (Fig. S4). WT border cells usually untrap themselves (Fig. S4).
We can use a simple calculation to analyze this problem (Fig. S5B). The energy cost of the untrapping move can be estimated to be proportional to the work done pushing the surrounding cells:
where P is the osmotic pressure in the nurse cells, and V is the volume of the cluster. The scale of the forces associated with this energy barrier can be estimated to be as follows:
We should compare this to the force of chemotaxis acting on the cluster, which we found to be the following:
Comparing and , we find that, below a critical radius , the chemotaxis force is too weak to overcome the trapping force, whereas above this critical size the chemotaxis force wins.
The critical radius increases with decreasing A, so for weaker chemotaxis signal, as we have in the PVR-DN case. Indeed, we see more trapping events here, which we may attribute to a larger critical size that occasionally comes close to the actual cluster radius. Remember that there is local variability in the trapping strength (represented by P) and strength of the chemotaxis signal and resultant cluster force (given by A).
SI Materials and Methods
To calculate the nurse cell untrapping time, SlboGal4, UAS-dsRedNLS; UAS-moesinGFP movies were taken using transmitted light detector (transmission–photomultiplier tube) to visualize nurse cell boundaries, and GFP/RFP GaAsP spectral detectors on a Zeiss LSM 780 microscope. Nurse cell junction is defined as a point along the border cell migration path where at least three nurse cell boundaries intersect, and is verified over multiple stacks in z direction. The process of border cells untrapping from nurse cell junction starts from when front of the cluster first touches the junction and ends when back of the cluster leaves it. We only looked at the junctions where border cell migration speed significantly decreased (26.3% of all junctions). We first masked the GFP channel with surface in Imaris, and then used BoundingboxAA (x direction) to measure cluster diameter. Cluster diameter is averaged over the time period when cluster is at nurse cell junction.
Supplementary Material
Acknowledgments
We thank Amy Peterson for assistance with movie tracking and Thomas Kenney for assistance with confocal microscopy. This work was supported by NIH Grant GM R01 46425 (to D.J.M.). N.S.G is the recipient of the Lee and William Abramowitz Professorial Chair of Biophysics, and acknowledges Israeli Science Foundation Grant 580/12 for support. We acknowledge the use of the Neuroscience Research Institute-Molecular, Cellular and Developmental Biology Microscopy Facility and the instrumentation supported by the Office of The Director, National Institutes of Health of the NIH under Award S10OD010610.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1522656113/-/DCSupplemental.
References
- 1.Parent CA, Devreotes PN. A cell’s sense of direction. Science. 1999;284(5415):765–770. doi: 10.1126/science.284.5415.765. [DOI] [PubMed] [Google Scholar]
- 2.Devreotes PN, Zigmond SH. Chemotaxis in eukaryotic cells: A focus on leukocytes and Dictyostelium. Annu Rev Cell Biol. 1988;4:649–686. doi: 10.1146/annurev.cb.04.110188.003245. [DOI] [PubMed] [Google Scholar]
- 3.Yu SR, et al. Fgf8 morphogen gradient forms by a source-sink mechanism with freely diffusing molecules. Nature. 2009;461(7263):533–536. doi: 10.1038/nature08391. [DOI] [PubMed] [Google Scholar]
- 4.Crick F. Diffusion in embryogenesis. Nature. 1970;225(5231):420–422. doi: 10.1038/225420a0. [DOI] [PubMed] [Google Scholar]
- 5.Moissoglu K, Majumdar R, Parent CA. Cell migration: Sinking in a gradient. Curr Biol. 2014;24(1):R23–R25. doi: 10.1016/j.cub.2013.10.075. [DOI] [PubMed] [Google Scholar]
- 6.Cai D, Montell DJ. Diverse and dynamic sources and sinks in gradient formation and directed migration. Curr Opin Cell Biol. 2014;30:91–98. doi: 10.1016/j.ceb.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Heit B, Tavener S, Raharjo E, Kubes P. An intracellular signaling hierarchy determines direction of migration in opposing chemotactic gradients. J Cell Biol. 2002;159(1):91–102. doi: 10.1083/jcb.200202114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen H, He Z, Bagri A, Tessier-Lavigne M. Semaphorin-neuropilin interactions underlying sympathetic axon responses to class III semaphorins. Neuron. 1998;21(6):1283–1290. doi: 10.1016/s0896-6273(00)80648-0. [DOI] [PubMed] [Google Scholar]
- 9.Lohof AM, Quillan M, Dan Y, Poo MM. Asymmetric modulation of cytosolic cAMP activity induces growth cone turning. J Neurosci. 1992;12(4):1253–1261. doi: 10.1523/JNEUROSCI.12-04-01253.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mosadegh B, et al. Generation of stable complex gradients across two-dimensional surfaces and three-dimensional gels. Langmuir. 2007;23(22):10910–10912. doi: 10.1021/la7026835. [DOI] [PubMed] [Google Scholar]
- 11.Meyvantsson I, Beebe DJ. Cell culture models in microfluidic systems. Annu Rev Anal Chem (Palo Alto, Calif) 2008;1:423–449. doi: 10.1146/annurev.anchem.1.031207.113042. [DOI] [PubMed] [Google Scholar]
- 12.Wang SJ, Saadi W, Lin F, Minh-Canh Nguyen C, Li Jeon N. Differential effects of EGF gradient profiles on MDA-MB-231 breast cancer cell chemotaxis. Exp Cell Res. 2004;300(1):180–189. doi: 10.1016/j.yexcr.2004.06.030. [DOI] [PubMed] [Google Scholar]
- 13.Venkiteswaran G, et al. Generation and dynamics of an endogenous, self-generated signaling gradient across a migrating tissue. Cell. 2013;155(3):674–687. doi: 10.1016/j.cell.2013.09.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pocha SM, Montell DJ. Cellular and molecular mechanisms of single and collective cell migrations in Drosophila: Themes and variations. Annu Rev Genet. 2014;48(1):295–318. doi: 10.1146/annurev-genet-120213-092218. [DOI] [PubMed] [Google Scholar]
- 15.Friedl P, Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat Rev Mol Cell Biol. 2009;10(7):445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 16.Theveneau E, et al. Collective chemotaxis requires contact-dependent cell polarity. Dev Cell. 2010;19(1):39–53. doi: 10.1016/j.devcel.2010.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Steinberg M. 1964. The problem of adhesive selectivity in cellular interactions. Cellular Membranes in Development. 22nd Symposium of the Society for the Study of Development and Growth (Academic, New York), pp 321–366.
- 18.Wolpert L. Positional information and the spatial pattern of cellular differentiation. J Theor Biol. 1969;25(1):1–47. doi: 10.1016/s0022-5193(69)80016-0. [DOI] [PubMed] [Google Scholar]
- 19.Grimm O, Coppey M, Wieschaus E. Modelling the Bicoid gradient. Development. 2010;137(14):2253–2264. doi: 10.1242/dev.032409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Montell DJ. Border-cell migration: The race is on. Nat Rev Mol Cell Biol. 2003;4(1):13–24. doi: 10.1038/nrm1006. [DOI] [PubMed] [Google Scholar]
- 21.Montell DJ, Rorth P, Spradling AC. slow border cells, a locus required for a developmentally regulated cell migration during oogenesis, encodes Drosophila C/EBP. Cell. 1992;71(1):51–62. doi: 10.1016/0092-8674(92)90265-e. [DOI] [PubMed] [Google Scholar]
- 22.Beccari S, Teixeira L, Rørth P. The JAK/STAT pathway is required for border cell migration during Drosophila oogenesis. Mech Dev. 2002;111(1-2):115–123. doi: 10.1016/s0925-4773(01)00615-3. [DOI] [PubMed] [Google Scholar]
- 23.Duchek P, Somogyi K, Jékely G, Beccari S, Rørth P. Guidance of cell migration by the Drosophila PDGF/VEGF receptor. Cell. 2001;107(1):17–26. doi: 10.1016/s0092-8674(01)00502-5. [DOI] [PubMed] [Google Scholar]
- 24.Duchek P, Rørth P. Guidance of cell migration by EGF receptor signaling during Drosophila oogenesis. Science. 2001;291(5501):131–133. doi: 10.1126/science.291.5501.131. [DOI] [PubMed] [Google Scholar]
- 25.McDonald JA, Pinheiro EM, Kadlec L, Schupbach T, Montell DJ. Multiple EGFR ligands participate in guiding migrating border cells. Dev Biol. 2006;296(1):94–103. doi: 10.1016/j.ydbio.2006.04.438. [DOI] [PubMed] [Google Scholar]
- 26.Prasad M, Montell DJ. Cellular and molecular mechanisms of border cell migration analyzed using time-lapse live-cell imaging. Dev Cell. 2007;12(6):997–1005. doi: 10.1016/j.devcel.2007.03.021. [DOI] [PubMed] [Google Scholar]
- 27.Bohlin T. On the Drag on a Rigid Sphere Moving in a Viscous Liquid Inside a Cylindrical Tube. Trans R Inst of Tech (Stockholm) 1960;155:1–63. [Google Scholar]
- 28.Vitorino P, Meyer T. Modular control of endothelial sheet migration. Genes Dev. 2008;22(23):3268–3281. doi: 10.1101/gad.1725808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cai D, et al. Mechanical feedback through E-cadherin promotes direction sensing during collective cell migration. Cell. 2014;157(5):1146–1159. doi: 10.1016/j.cell.2014.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Reffay M, et al. Orientation and polarity in collectively migrating cell structures: Statics and dynamics. Biophys J. 2011;100(11):2566–2575. doi: 10.1016/j.bpj.2011.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gov NS. Traction forces during collective cell motion. HFSP J. 2009;3(4):223–227. doi: 10.2976/1.3185785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ben-Isaac E, et al. Effective temperature of red-blood-cell membrane fluctuations. Phys Rev Lett. 2011;106(23):238103. doi: 10.1103/PhysRevLett.106.238103. [DOI] [PubMed] [Google Scholar]
- 33.Malet-Engra G, et al. Collective cell motility promotes chemotactic prowess and resistance to chemorepulsion. Curr Biol. 2015;25(2):242–250. doi: 10.1016/j.cub.2014.11.030. [DOI] [PubMed] [Google Scholar]
- 34.Llense F, Martín-Blanco E. JNK signaling controls border cell cluster integrity and collective cell migration. Curr Biol. 2008;18(7):538–544. doi: 10.1016/j.cub.2008.03.029. [DOI] [PubMed] [Google Scholar]
- 35.Melani M, Simpson KJ, Brugge JS, Montell D. Regulation of cell adhesion and collective cell migration by hindsight and its human homolog RREB1. Curr Biol. 2008;18(7):532–537. doi: 10.1016/j.cub.2008.03.024. [DOI] [PubMed] [Google Scholar]
- 36.Liu Y, Montell DJ. Identification of mutations that cause cell migration defects in mosaic clones. Development. 1999;126(9):1869–1878. doi: 10.1242/dev.126.9.1869. [DOI] [PubMed] [Google Scholar]
- 37.Bai J, Montell D. Eyes absent, a key repressor of polar cell fate during Drosophila oogenesis. Development. 2002;129(23):5377–5388. doi: 10.1242/dev.00115. [DOI] [PubMed] [Google Scholar]
- 38.Fraley SI, et al. A distinctive role for focal adhesion proteins in three-dimensional cell motility. Nat Cell Biol. 2010;12(6):598–604. doi: 10.1038/ncb2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stonko DP, Manning L, Starz-Gaiano M, Peercy BE. A mathematical model of collective cell migration in a three-dimensional, heterogeneous environment. PLoS One. 2015;10(4):e0122799. doi: 10.1371/journal.pone.0122799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ma EY, Raible DW. Signaling pathways regulating zebrafish lateral line development. Curr Biol. 2009;19(9):R381–R386. doi: 10.1016/j.cub.2009.03.057. [DOI] [PubMed] [Google Scholar]
- 41.Kuriyama S, et al. In vivo collective cell migration requires an LPAR2-dependent increase in tissue fluidity. J Cell Biol. 2014;206(1):113–127. doi: 10.1083/jcb.201402093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Herzmark P, et al. Bound attractant at the leading vs. the trailing edge determines chemotactic prowess. Proc Natl Acad Sci USA. 2007;104(33):13349–13354. doi: 10.1073/pnas.0705889104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Haeger A, Wolf K, Zegers MM, Friedl P. Collective cell migration: Guidance principles and hierarchies. Trends Cell Biol. 2015;25(9):556–566. doi: 10.1016/j.tcb.2015.06.003. [DOI] [PubMed] [Google Scholar]
- 44.Cheung KJ, et al. Polyclonal breast cancer metastases arise from collective dissemination of keratin 14-expressing tumor cell clusters. Proc Natl Acad Sci USA. 2016;113(7):E854–E863. doi: 10.1073/pnas.1508541113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Prasad M, Wang X, He L, Montell DJ. Cell Migration: Developmental Methods and Protocols. Springer; New York: 2011. Border cell migration: A model system for live imaging and genetic analysis of collective cell movement; pp. 277–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schindelin J, et al. Fiji: An open-source platform for biological-image analysis. Nat Methods. 2012;9(7):676–682. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.