Abstract
EphA1 is a receptor tyrosine kinase (RTK) that plays a key role in developmental processes, including guidance of the migration of axons and cells in the nervous system. EphA1, in common with other RTKs, contains an N-terminal extracellular domain, a single transmembrane (TM) α-helix, and a C-terminal intracellular kinase domain. The TM helix forms a dimer, as seen in recent NMR studies. We have modeled the EphA1 TM dimer using a multiscale approach combining coarse-grain (CG) and atomistic molecular dynamics (MD) simulations. The one-dimensional potential of mean force (PMF) for this system, based on interhelix separation, has been calculated using CG MD simulations. This provides a view of the free energy landscape for helix–helix interactions of the TM dimer in a lipid bilayer. The resulting PMF profiles suggest two states, consistent with a rotation-coupled activation mechanism. The more stable state corresponds to a right-handed helix dimer interacting via an N-terminal glycine zipper motif, consistent with a recent NMR structure (2K1K). A second metastable state corresponds to a structure in which the glycine zipper motif is not involved. Analysis of unrestrained CG MD simulations based on representative models from the PMF calculations or on the NMR structure reveals possible pathways of interconversion between these two states, involving helix rotations about their long axes. This suggests that the interaction of TM helices in EphA1 dimers may be intrinsically dynamic. This provides a potential mechanism for signaling whereby extracellular events drive a shift in the repopulation of the underlying TM helix dimer energy landscape.
The Eph receptors play an important role in developmental processes including cell migration and axonal guidance.1 This group of receptors is the largest of the receptor tyrosine kinase (RTK) family. The RTKs can be activated through the binding of extracellular ligands. In the case of Eph receptors, there are two classes of receptors, A and B, which mainly interact with the ligands ephrin A and B, respectively; cross-interactions between EphA receptors and ephrins B have also been reported.2,3 The binding of ligand leads to the creation of receptor oligomers (dimers and/or higher order oligomers).4 There is also growing evidence that RTKs also form (inactive) dimers in the absence of ligands. This preformed and inactive dimeric configuration has been discussed for several RTKs,5,6 including the EGFR7 and FGFR,8 and has sometimes been referred to as a pre-dimerization state.9 For EphA2, data also support ligand-independent clustering of the receptor.10,11 Furthermore, it has been postulated that Eph receptor dimers can switch between active and inactive configurations through a rotation coupling activation mechanism,12,13 and indeed recent mutational experiments highlighted more or less activated forms of the dimer compared to the wild-type EphA2 receptor in both ligand-dependent and -independent configurations.14 Taken together, these studies emphasize the importance of a better understanding of how EphA2 and related receptors may adopt alternative dimeric configurations and of how they may pass from one dimeric configuration to another.
The structure of Eph receptors is typical for RTKs. It is composed of an extracellular region that interacts with ephrin ligands10,15 and an intracellular region containing a juxtamembrane region, a tyrosine kinase domain, and a steril-alpha motif (SAM) domain, often followed by a PDZ binding motif. The two regions are linked by a transmembrane (TM) helix. This TM helix plays a role in the dimerization of the Eph receptor,12,13,16 a feature shared by numerous receptor tyrosine kinases (RTKs17). Several studies have emphasized the role of the TM helix dimer and changes in its packing mode in signaling by RTKs including EGFR7,18 and FGFR319,20 in addition to other cellular receptors21 including the insulin receptor.22 In particular, recent mutational studies of the closely related EphA2 receptor have suggested that switching of the TM helix dimer between two packing modes is a possible mechanism underlying EphA2 signal transduction.14 Given that association of TM helix domains23−25 is central to RTK signaling, understanding the nature of TM helix association is a necessary component of understanding mechanisms of signaling.9
Structures of EphA1 and of EphA2 TM helix dimers in phospholipid bicelles have been determined using NMR.12,13 The EphA1 TM domain forms a right-handed helix dimer interacting via an N-terminal glycine zipper motif (A550X3G554X3G558;12 see also the sequence in Figure 1). The importance of the Small-X3-Small motif was highlighted more than 20 years ago in growth factor receptors.26 It is the main interaction motif of the first NMR structure determined for a TM helix dimer (in glycophorin A27) and has since been studied and identified in numerous TM domains.28 Although there is a high frequency of glycine and small residues in the 58 TM helix sequences of the human RTKs,29 direct conservation of a common interaction motif is not apparent. This diversity may reflect differences in local structure of the TM domains and/or different modes of activation for each RTK. Thus, the interaction through the Small-X3-Small motif is not the only mode of association available to TM domains.25 Indeed, the EphA2 TM domain has been shown to dimerize via a heptad repeat motif.13 On this basis, it has been suggested that changes in helix packing mode may underlying signaling mechanisms by EphA and related receptors, with interactions via different motifs corresponding to active and inactive states of the receptor.14
Figure 1.
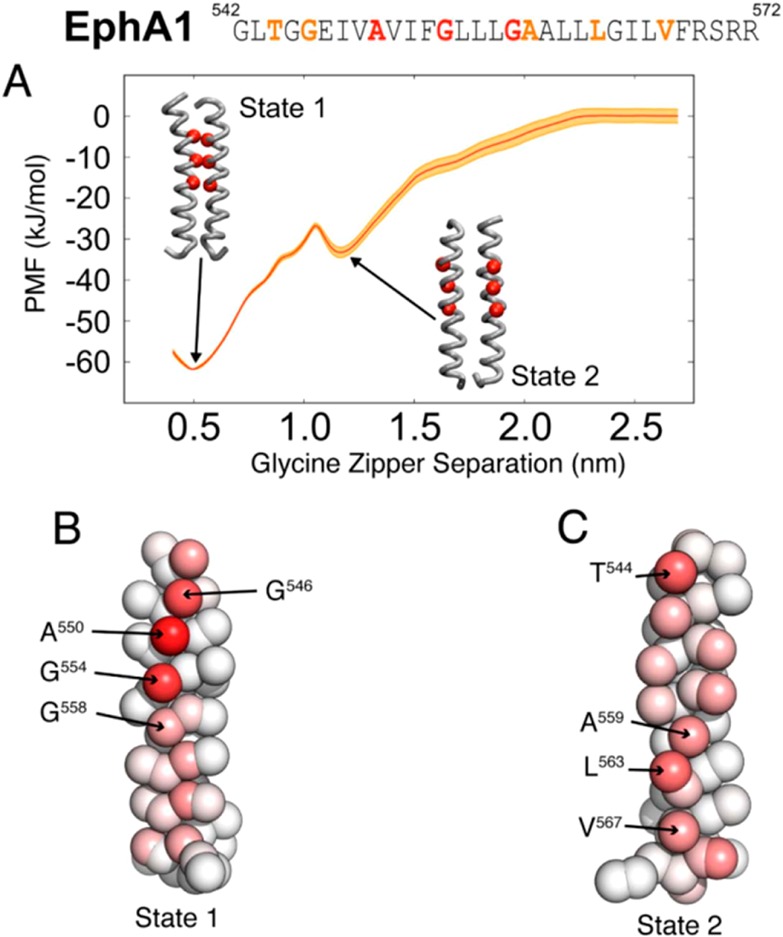
(A) PMF profile for the EphA1 TM helix dimer. The reaction coordinate is the separation of the centers of mass of the glycine zipper motifs. A stable minimum is seen at a glycine zipper separation of 0.5 nm (State 1), corresponding to the NMR configuration. A metastable state is seen at a glycine zipper separation of 1.2 nm (State 2). The error estimation of the PMF profile (red curve) is superimposed in orange. Above the PMF profile, the sequence of the EphA1 TM domain, from G542 to R572, is shown, with residues forming the glycine zipper in red and additional residues involved in the dimer interaction presented in (B) and (C) in orange. (B, C) The EphA1 TM helix, in CG representation, with particles colored according to the fraction of the simulation for which the particle was one of the closest five particles to its corresponding particle on the other helix for the simulation windows corresponding to (B) State 1 and (C) State 2. Red corresponds to a particle that was one of the closest five particles to its corresponding particle on the other helix for the whole simulation; white corresponds to a particle that was never one of the closest five particles to its equivalent particle on the other helix.
A number of experimental techniques exist for measuring association of TM helices,30 including TOXCAT and related assays,29,31 biophysical approaches including FRET,32 and analytical ultracentrifugation.33,34 Computational methods (including molecular dynamics (MD) or Monte Carlo (MC) simulations) provide a complementary approach for exploring the energy landscapes for association of TM helix dimers and have been applied to model systems such as the TM domain of glycophorin A.35−37 Simulation approaches have more recently been applied to studying TM helix dimers from RTKs such as ErbB.38,39 Polyansky et al. have suggested a modeling framework to predict and analyze TM dimer interaction in which MD simulations and potential of mean force (PMF) calculations play a central role.40 A number of these studies have employed coarse-grained (CG) models41,42 and have shown that CG models yield similar free energies of dimerization to those from more detailed atomistic simulations of the well-studied glycophorin A TM helix dimer (compare, e.g., refs (35) and (36)). Recent studies of, e.g., the integrin TM helix dimer,43 glycophorin A,44 and the protein adaptor DAP1245 have shown that by combining CG and atomistic simulations a detailed view of the nature of helix/helix interactions in TM helix dimers may be obtained.
In this study, we explore the EphA1 TM domains using MD simulations in order to gain insights into their mechanism of dimerization and how it may effect the activation of the receptor. There have been a number of MD studies of the dimerization of EphA1 receptor TM domain.12,40,46,47 Here, we have used CG MD simulations to calculate a one-dimensional free energy landscape for the association of the EphA1 TM domain in a phospholipid bilayer. This suggests two metastable states for this system, consistent with recent results for other RTKs and with models of the activation mechanism involving alternative packing modes of the TM helices. We have used unrestrained MD simulations to compare representative models from the free energy calculations with the NMR structure of the dimer. These simulations suggest a pathway for interconversion of the two packing modes via rotation of the TM helices, which, in turn, may provide a pathway to link a potential inactivate configuration to the activated state of the receptor. Atomistic simulations of representative structures from the CG energy landscape allow refinement of these models and provide a more detailed description of the underlying helix–helix interactions.
Methods
Unrestrained CG Simulations Starting from the NMR Structure
The NMR structure of the EphA1 dimer (PDB ID: 2K1K)12 was converted into a CG model. Titratable amino acids were in their default ionization states. The CG force field used was a local modification48,49 of the widely employed MARTINI force field.41,42 A harmonic restraint was applied to backbone particles to mimic secondary structure stabilizing hydrogen bonds, with an equilibrium bond length of 0.6 nm and a force constant of 1000 kJ/mol/nm2. We then added 269 DPPC (or DLPC) lipids, water molecules, and counterions using the self-assembly method.50,51 After an initial 5000 steps of steepest descent energy minimization, the simulation was run for 100 ns to allow the lipids to self-assemble around the protein. All simulations were performed using GROMACS (http://www.gromacs.org/).52 A Berendsen thermostat was used with a coupling constant of 1.0 ps. The reference temperature was 323 K. Electrostatic interactions utilized a relative dielectric constant of 20. Lennard–Jones and electrostatic interactions were shifted to zero between 0.9 and 1.2 nm and 0 and 1.2 nm, respectively. A Berendsen barostat with a coupling constant of 1.0 ps, a compressibility value of 5.0 × 10–6 bar–1, and a reference pressure of 1 bar was used. The integration time step was 10 fs.
PMF Calculations
As described above, we performed CG MD simulations to yield a structure of the EphA1 dimer. This structure was subsequently used as a starting point for PMF calculations. Thus, we initially ran a 200 ns CG MD simulation during which 271 DPPC lipids were allowed to self-assemble to form a bilayer around a pair of restrained TM helices (aligned with their long axes parallel to the z axis and separated by 7 nm). Titratable amino acids were in their default ionization states. Five 1.5 μs simulations were subsequently performed with these helices unrestrained, yielding dimers interacting through their glycine zipper motifs. One such dimer was then used as a starting point for PMF calculations, increasing the separation of the centers of mass of the glycine zipper motifs as the PMF reaction coordinate.
The PMF was calculated using the umbrella sampling technique.53 Twenty-four independent simulations, each of 7.5 μs in duration, were run for the PMF calculation, i.e., the simulations corresponding to the 24 windows were run such that the initial configuration of one simulation did not depend on the outcome of the preceding simulation. Each independent simulation corresponds to a different separation distance of the center of mass of the glycine zipper motifs on each helix. The time step was 40 fs, and the reference temperature was 323 K. The starting structure for each window in a given calculation was the same. The center of mass of the chosen motif was restrained along both axes in the plane of the bilayer. The restraint was harmonic with a force constant of 1000 kJ/mol/nm2. In one axis (y), the restraint was centered around zero separation in each window. Along the other axis (x), the center of the restraint varied from 0.4 to 2.7 nm, in 0.1 nm intervals. The restraints were applied to the chosen motifs of the starting structure at the beginning of the simulation; the helices moved rapidly (within 5 ns) to the vicinity of the center point of restraint for all windows. It is important to note that the separation of the two helices, i.e., the starting point to launch each simulation is set independently of the other adjacent simulations. Thus, during each simulation, there is directional increment in the initial separation: there is only a constraint on the distance between the two helices. To estimate the convergence of the system, we have used the approach of Yang et al.54 Then, the PMF profile was calculated using the weighted histogram analysis method (WHAM)55 as implemented by Grossfield (http://membrane.urmc.rochester.edu/content/wham/, version 2.0.9), and errors were estimated using the uncorrelated data (see Supporting Information, text and Figure S1). For unrestrained CG simulations, we used either systems extracted from the (restrained) PMF simulations or CG models derived from the NMR structure.
Structure Selection for AT Simulations
From NMR Structures in DPPC Bilayer
We performed clustering on all of the trajectories using the g_cluster tool with a cutoff of 0.2 nm. This analysis revealed 2 different configurations. The major cluster (representing 95% of the ensemble of trajectories) corresponded to the helices interacting via the glycine motif. The representative structure for this cluster was extracted from run 4 based on the NMR structure. The second cluster represents only 3% of the whole population and defined an intermediate state between States 1 and 2 (see Results below for the definition of these states). This structure was characterized by a glycine zipper distance around 0.9 nm and a crossing angle around −10°.
From PMF Structures
We have extracted the last frame from one run of the CG simulation to depict State 1 (see Supporting Information Figure S3A). This structure had a crossing angle around −20°, and the glycine zipper distance was around 0.5 nm. For State 2, we selected the most representative structure from the unrestrained simulation with a crossing angle based on a structure centered around −5°. This structure has a glycine zipper distance around 1.2 nm.
AT Simulation Details
The conversion from CG models to AT representations was as described previously.56 This method uses a fragment-based protocol to convert CG protein and lipid molecules. Water and counterions molecules were added to equilibrate the systems. For each converted system, a 5000 step steepest descent minimization was performed followed by an equilibration phase. For this equilibration, we gradually decreased the restraints on the protein backbone, passing from a constant of 1000 to 250 kJ/mol/nm2 in 4 ns. We then completely removed restraints to run production simulations for a duration of 50 to 70 ns, depending of the system. The simulations were performed using the GROMOS96 43a1 force field. Long-range electrostatic were modeled up to 0.1 nm using the particle mesh Ewald (PME) method.57 The same cutoff distance was used to model van der Waals interaction. The reference temperature was 323 K. All simulations were performed at constant temperature, pressure, and particle number using semi-isotropic pressure coupling with the Parinello–Rahman barostat58 and the V-rescale thermostat.59 The integration time step was 2 fs. We also created a system with a single EphA1 TM helix in a DPPC bilayer using as a starting point a CG model of ideal α-helix embedded in the bilayer using the self-assembly methodology described before. This was then converted to an AT representation and used to launch a 1.2 μs simulation.
Analysis
Representative structures of the dimer were obtained using the g_cluster tool. Contact analysis was performed on simulations that corresponded to low-energy states on the relevant PMF profiles. The fraction of the simulation for which each residue was in the closest 5 residues to its partner on the opposing helix was calculated. Crossing angles, interhelix distances, and residue contact calculations were performed using locally written code.60 Structure visualization and some analysis were also performed using VMD.61
Results
Stability of a Single EphA1 Transmembrane Helix
To avoid biasing our simulation by using the structure of an EphA1 helix extracted from the NMR dimer structure (PDB ID: 2K1K), we instead used an ideal α-helix model to depict the TM domain. To evaluate the stability of this structure, we performed a long (1.2 μs) AT simulation of the single helix inserted in a DPPC bilayer. Using the do_dssp utility from GROMACS, we analyzed the secondary structure of the TM domain as a function of time (see Supporting Information Figure S2A). For the first 0.3 μs, the α-helix was stable (apart from the two extremities switching between helix and coil). Subsequently, we observed transient changes in helicity, but overall the secondary structure of the TM domain stayed stable throughout the simulation. These transient changes may reflect limitations of the force field, as revealed in long simulations.62 Due to the relative simplicity of the CG model, we considered that an ideal α-helix was a good starting model for the EphA1 TM domains to be used in our subsequent PMF calculations.
A Free Energy Landscape for Helix–Helix Interactions
To understand the free energy landscape for helix–helix interactions within a EphA1 TM helix dimer, we undertook potential of mean force (PMF) calculations based on a reaction coordinate corresponding to interhelix separation. These were aimed to provide a (one-dimensional) profile of the free energy of interaction of a pair of parallel EphA1 TM helices in a lipid bilayer as a function of the interhelix separation. As a prelude to these calculations, we performed five simulations (each of 1.5 μs duration) starting from two parallel EphA1 TM helices inserted initially 7 nm apart in a CG bilayer containing 271 DPPC molecules. A dimer was formed in each of these five self-assembly simulation within 20–800 ns. In four of the five simulations, the helices interacted via their N-terminal glycine zipper motifs (i.e., A550X3G554X3G558), as is the case in the NMR structure. (One self-assembly simulation did not yield a stable dimer.)
On the basis of the self-assembly simulations, we used a TM dimer in which the helices interacted via the N-terminal glycine zipper motif as the starting point for the PMF calculation. In these calculations, we progressively moved the two helices apart, using the separation of the centers of mass of their glycine zipper motifs as the PMF reaction coordinate. These configurations were used as starting points to launch 24 independent simulations, each of 7.5 μs in duration, with each corresponding to a glycine zipper separation window of width 0.1 nm with the reaction coordinate ranging from 0.4 to 2.7 nm (Figure 1A). The profile shows a globally stable state at a glycine zipper separation of 0.5 nm, which we will refer as State 1. The profile also shows a metastable state at a glycine zipper separation of 1.2 nm, which we will call State 2. Cluster analysis was used to produce a representative structure of each state. In the State 1 structure, the glycine zippers pack against one another (Figure 1B). In contrast, in State 2, the glycine zipper motifs face away from each other. Thus, State 1 is similar to the NMR structure of the EphA1 TM dimer.12 In State 2 (Figure 1C), the helix–helix interactions are predominantly via residues T544, A559, L563, and V567. Thus, the one-dimensional free energy landscape suggests at least two possible modes of interaction of the TM helices within an EphA1 TM helix dimer.
To help understand the differences between the two states, we analyzed helix crossing angles and the structural dynamics of the two restrained dimer simulations (Figure 2), i.e., of the two 7.5 μs simulation trajectories for the glycine zipper separation at 0.5 nm (State 1) and 1.2 nm (State 2). For State 1, the main crossing angle is −21° (Figure 2A,B), corresponding to right-handed helix packing. Significantly, two minor populations are seen with crossing angles of −3° and +3°, and the time course of the crossing angle shows frequent switching among all three crossing angles. For the State 2 simulation, two overlapping major populations are seen, with crossing angles of −5° and +3° (Figure 2A,B). Thus, it can be seen that even in the restrained simulations corresponding to individual “states” along the free energy profile there is flexibility in the helix–helix interactions, as indicated by the multimodal helix crossing angle distributions.
Figure 2.
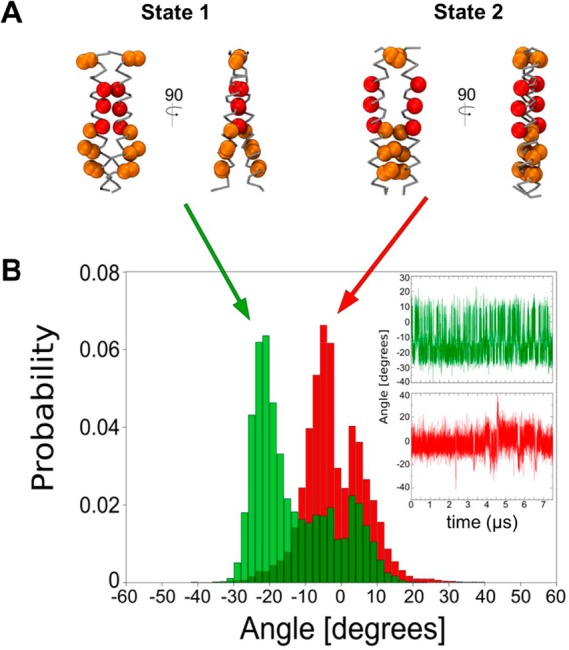
(A) The most representative structures for States 1 and 2 with helix crossing angles of −21° and −5°, respectively. The glycine motif residues are shown in red. (B) Helix crossing angle distribution based on 7.5 μs restrained simulations starting from State 1 (green) and State 2 (red). The insets on the right show the corresponding helix crossing angles as a function of time. Note that we have calculated the crossing angle from residue Val549 to Val567 on each helix to limit the calculation to the helix core.
Unrestrained CG Simulations of the State 1 and State 2 Structures
To further characterize the dynamic behavior of the two states (and also to check that artifacts were not introduced by the reaction coordinate restraint in the PMF calculations63), we used several representative structures extracted from each state (three for State 1 and two for State 2; see Figure 2A and Supporting Information Figure S2B) as starting points for unrestrained CG simulations, each of 1 μs in duration. Starting from three State 1 structures (selected to correspond to the three peaks in the crossing angle distribution in Figure 2B; see above), the three unrestrained simulations yielded comparable crossing angle distributions, with a major population corresponding to a crossing angle of −21° and two minor populations peaks at −3° and +3° (Figure 3A). Thus, these crossing angle distributions are the same as that derived from the State 1 window of the restrained PMF simulations (see also Supporting Information. S3A). For the two representative structures extracted from State 2, one of the unrestrained simulations yielded a population with a main crossing angle of −5°, i.e., the same as that from the State 2 window of the restrained PMF simulations. Nevertheless, due to the relatively short time simulation, we cannot exclude that, after a longer simulation time, the TM domain may pass from the metastable State 2 to the more stable State 1.
Figure 3.
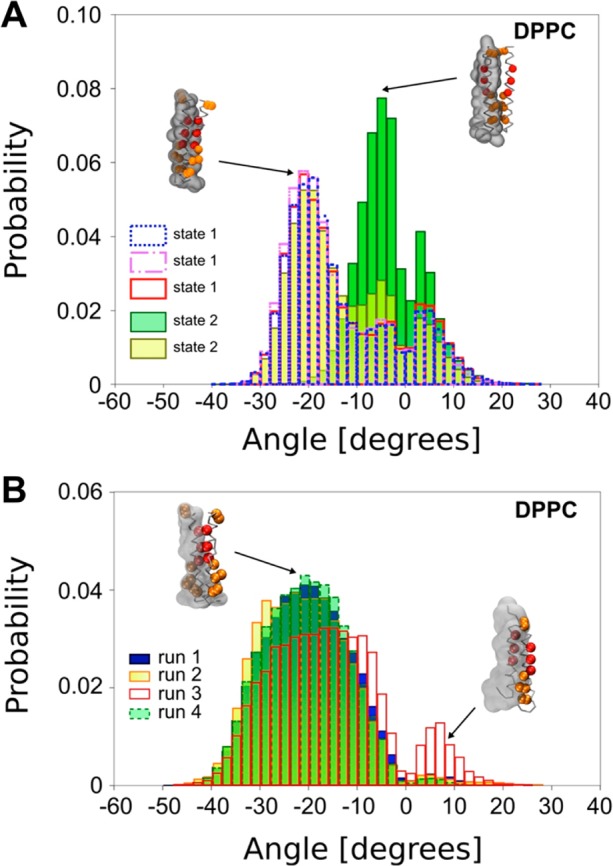
(A) Helix crossing angle distributions based on the 1 μs unrestrained dynamics for the most representative structures for States 1 and 2 in a DPPC bilayer. (B) Helix crossing angle distribution for the four simulations (each of 1 μs in duration) using the NMR structure of the EphA1 dimer in a DPPC bilayer. Inset figures show the dimer structure, with red particles depicting residues forming the glycine zipper and orange particles showing additional residues involved in the dimer interaction for State 2. The transparent envelope depicts the surface of one CG helix.
Indeed, the second unrestrained simulation starting from a State 2 structure (with a crossing angle of +3°) leads to a clear switch to a distribution of crossing angles similar to those seen when starting from State 1, with a major population centered around −20° (Figure 3A). Examining the crossing angle as a function of the time revealed a shift (at around 200 ns) from a value centered around 0 to one centered around −20°, i.e., from State 2-like behavior to State 1-like behavior (see Supporting Information Figure S3A). We have repeated this simulation three more times, changing initial random velocity seeds, and in each case observed the same behavior (see Supporting Information Figure S4).
We further analyzed the four unrestrained simulations that showed a transition from crossing angles centered around 0° to crossing angles centered around −20° in terms of the distance between centers of mass of helices and of the residues in contact along these trajectories (Figure 4; also see Supporting Information Figure S5). This revealed that the EphA1 TM helix dimer can indeed switch from a structure in which the glycine zipper is pointing away from the helix–helix interface (i.e., State 2) to a structure in which this motif forms the interface (i.e., State 1). This transition from State 2 to State 1 passes through an intermediate conformation in which residues involved in the State 2 interface (A559, L563, and V567) are not completely released, whereas the residues comprising the glycine motif (i.e., A550, G554, and G558) interact together (Supporting Information Figure S5A between 530 and 715 ns and Figure S5B,C after 153.5 and 117 ns).
Figure 4.
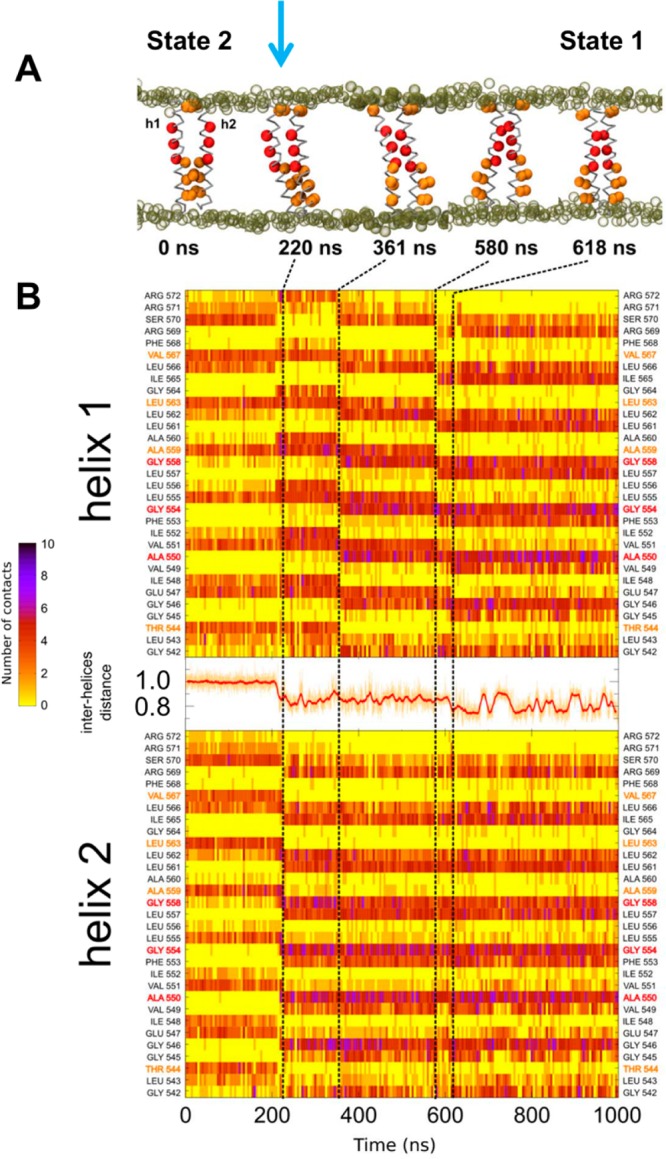
Detailed view of one of the unrestrained simulations (duration 1 μs) starting from a State 2 structure, with the vertical arrow at ca. 220 ns indicating the start of a switch to State 1. (A) Snapshots of the dimer illustrating the progress of the simulation. Red particles depict residues forming the glycine zipper, and orange particles represent residues involved in the C-terminal dimer interaction seen in State 2. Tan empty spheres represent the phosphate groups of the lipid molecules. (B) Diagrams depicting the number of contact at the dimer interface as a function of residue number (vertical axis) and time (horizontal axis). In between the helix 1 and helix 2 diagrams, the red curve shows the interhelix distance as a function of time.
The transition between the two main states is also seen if one tracks the distance between the centers of mass of each helix (Figure 4B). Thus, for State 1, this distance fluctuates between ca. 0.8 and 0.9 nm (see Figure 4B after 620 ns and Supporting Information Figure S5A after 715 ns). In contrast, for State 2, the interhelix distance averages ca. 1.0 nm and exhibits only small fluctuations (see the first 200 ns in Figure 4B).
Unrestrained CG Simulations Based on the NMR Structure
It has been suggested that the EphA1 dimer may adopt multiple conformations.64 In the context of this and our observations of switching between the two states defined by the PMF calculations, we performed CG MD simulations starting from the NMR structure (2K1K) of the EphA1 TM dimer embedded in a lipid bilayer. The results show that over 1 μs of CG MD simulation the distribution of crossing angles exhibit a major population centered around −20° (Figure 3B), i.e., the same major population as that for the State 1 simulations. This is not surprising, as both the State 1 and the NMR structures exhibit right-handed crossing angles and in both structures the helices interact via the glycine zipper motif. The crossing angle for the initial NMR dimer is somewhat larger (ca. −30°) than the modal value of −20° seen for the simulations, but the experimental value is clearly within the range observed in either the unrestrained State 1 or the NMR-structure-based simulations. The structures within the NMR-based simulations remained close to the initial NMR structure. Thus, the average Cα RMSD from the NMR structure is 0.43 nm, although, of course, there were considerable dynamic fluctuations during the simulations, with RMSDs ranging from 0.2 to 0.7 nm. Significantly, the representative structure of State 1 (see above) had a Cα RMSD of 0.46 nm from the NMR structure, suggesting that the PMF-based and NMR-based simulations were sampling the same region of conformational space.
Interestingly, in all of the simulations initiated from the NMR structures (especially in run 3 in Figure 3B), a minor population was observed with a positive crossing angle, i.e., left-handed packing of the helices. On closer inspection, it can be seen that this minor population corresponds to an asymmetric dimer. In this asymmetric dimer, one helix interacts through its glycine zipper motif, whereas the other helix interacts mainly via residues of the State 2 interface, i.e., A559, L563, and V567. (Indeed, this asymmetric dimer conformation constituted the main population for one simulation in NMR structure initiated simulations in a thinner, DLPC, bilayer; see Supporting Information Figures S3C and S6.) Thus, CG MD simulations based either on the PMF-derived stable and metastable states or on the NMR structure reveal complex and dynamic behavior of the EphA1 TM dimer, involving both the canonical glycine zipper interface as well as a more C-terminal interface and an asymmetric conformation. Interestingly, two recent computational studies of the conformational dynamics of the EphA1 TM dimer reveal comparable behavior.46,64 Both of these studies also found the most stable state to correspond to the NMR structure (i.e., a right-handed, glycine-zipper-mediated packing of the helices). Interestingly, the simulations of Li et al. (using an implicit bilayer model) also revealed a left-handed dimer conformation with a leucine zipper interaction motif.64
Two-Dimensional Conformational Landscape for TM Helix Dimers
To characterize the pathway(s) between the two states, we generated a map of the conformational landscape as a function of crossing angle and the glycine zipper interhelix separation from the multiple restrained simulation trajectories used for the PMF calculations. It is also useful to map the unrestrained CG simulations onto this crossing angle/separation landscape (Figure 5). For the unrestrained simulations starting from State 2 models (Figure 5A), after fluctuations between −10° and +10° at a separation of ca. 1.2 nm (i.e., State 2 behavior), the structures switch to a separation of ca. 0.5 nm with a crossing angle fluctuating around ca. −20° (i.e., State 1 behavior). We also note that the trajectory of the switch between States 1 and 2 passed through an area centered on a glycine motif separation of 0.8 nm and corresponding to the asymmetric dimer. This path broadly follows the more populated areas of the underlying 2D map. For the NMR structure initiated simulations (Figure 5B), in three of the simulations the helix dimer stayed mainly in the State 1 region of the map (i.e., at a separation ca. 0.5 nm with fluctuations in the crossing angle between −40° and +10°), whereas for the fourth (run 3 in Figure 3B) simulation, the dimer evolved to a separation of ca. 0.9 nm, again following the underlying 2D landscape, corresponding to an asymmetric intermediate between States 1 and 2. Thus, the 2D map of the conformational landscape of the unrestrained simulations is globally in agreement with possible pathway(s) for interconversion involving an asymmetric dimer (separation ca. 0.8 nm) intermediate between the stable between the stable (State 1) and metastable (State 2) states identified from the one-dimensional PMF.
Figure 5.
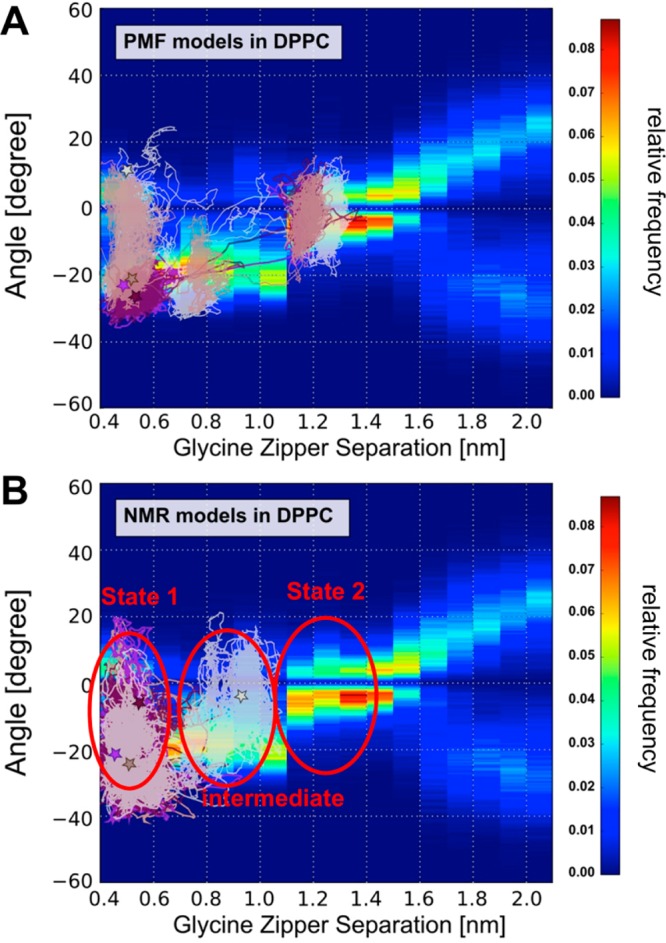
(A) The trajectories of the unrestrained CG simulations starting from the PMF-generated structure of State 2 are shown on top of the conformational map from the (restrained) PMF simulations. Thus, the map of the conformational landscape of the helix dimer is shown as a function of crossing angle and the glycine zipper interhelix separation. This map was obtained from the different trajectories used for the PMF calculations. For each 0.1 nm window from the set of PMF trajectories, the crossing angle was calculated, and the relative frequencies are shown on a blue–green–red colorscale. (B) The trajectories of the unrestrained CG simulations starting from the NMR structure are shown on top of the same conformation map as in (A). Stars depict the final configuration of the dimer for each trajectory. In plotting these trajectories, we sample averaged positions (based on 10 steps) every 0.5 ns.
A (Simplified) Model for Interconversion Between States 1 and 2
On the basis of the simulations and analysis presented above, we can propose a (simplified) model for interconversion between the two major states of the EphA1 TM helix dimer, as summarized in Figure 6, in which States 1 and 2 may interconvert via an ensemble of intermediate states that have a glycine zipper separation of ca. 0.8 nm and that includes asymmetric helix dimers. This suggests that the repacking of the dimer may occur via mechanisms of either concerted or decoupled rotations. In the case of the concerted rotation pathway, the upper parts of the dimer (i.e., residues from T544 to A559) undergo a combined sliding and rotation movement, leading to the creation of the glycine zipper (Supporting Information Figure S5 and Movie S1). This yields an intermediate structure in which the glycine zipper interacts at the dimer interface in addition to residues L555, A559, L563, or A567. The interconversion of States 1 and 2 can also occur via decoupled rotations. In this case, one helix rotates (e.g., Figure 4A and Supporting Information Movie S2) to create an asymmetric dimer (as also seen in our simulations based on the NMR structure) and subsequently the second helix switches to form an alternative symmetric dimer. Thus, in both cases, rotational motions about the helix axes provide a potential mechanism for interconversion of States 1 and 2.
Figure 6.
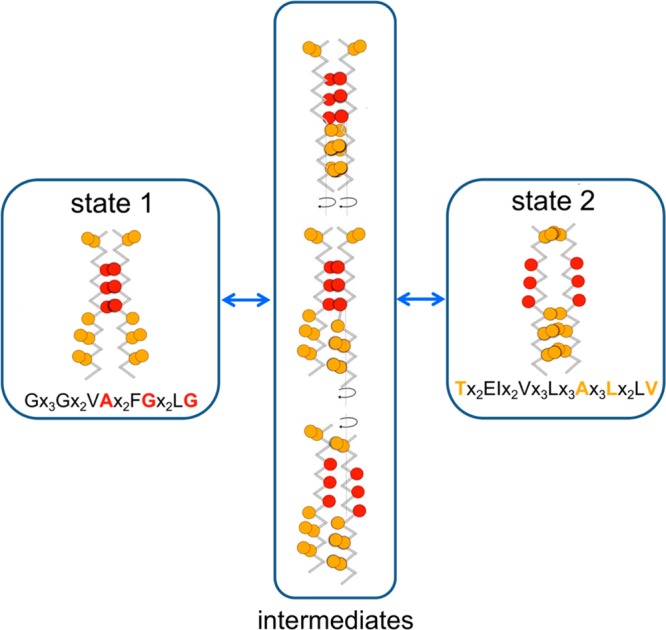
Schematic representing the putative pathway(s) of interconversion between States 1 and 2 derived from the unrestrained dynamics simulations. See main text for further details.
Model Refinement with Atomistic Simulations
To increase the resolution of our description of the two TM dimer states and their dynamic properties, we selected representative structures from the CG simulations and converted them to atomistic resolution (see Methods). Thus, two structures from the unrestrained CG simulations (one structure representing State 1 and the other, State 2; see Supporting Information for details of the structure selection method) and also two structures from the NMR-based CG simulations were selected. These four systems (protein and lipids) were converted to atomistic models.56 For each resultant system, we performed a short (50 ns) AT-MD simulation (which was extended to 70 ns for the model based on State 2 to obtain a stable structure). For each of the four simulations, the dimer structure evolved during the first few nanoseconds (the Cα RMSD increasing between 0.25 and 0.45 nm). The State 1 model and the two NMR initiated simulations all retained a negative crossing angle (i.e., right-handed packing), whereas the State 2 model retained a crossing angle of ca. 0° throughout their respective atomistic simulations.
The atomistic simulations reveal exploration of the crossing angle versus glycine zipper distance landscape even though the time scale was small in comparison of with the CG simulations. Nevertheless, the AT simulations agree quite well with the (CG) map of the landscape (see Supporting Information Figure S7). Furthermore, the AT simulations explored a substantial range in term of glycine zipper separation, covering the majority of the distance range seen in the CG simulations. Thus, the simulation started from a structure from the NMR run 4 CG simulation described the State 1 configuration with a glycine zipper distance mostly around 0.5 nm and a crossing angle centered around −20°. The residues at the interface are mainly from the motif G546X3A550X3G554X3G558, along with some interactions of residues F553, L557, I559, and I565 (Figure 7A). The AT simulations starting with structures from PMF State 1 and NMR run 3 described an intermediate state between States 1 and 2 in which residues involved in the glycine motif as well as some residues involved in State 2 packing were present at the interface (Figure 7B; also see Supporting Information Figure S8). In particular, these two simulations reveal that residues T544 and of E547 can form inter- and intrahelix hydrogen bonds (see Supporting Information Table S1 and Figures S9 and S10).
Figure 7.
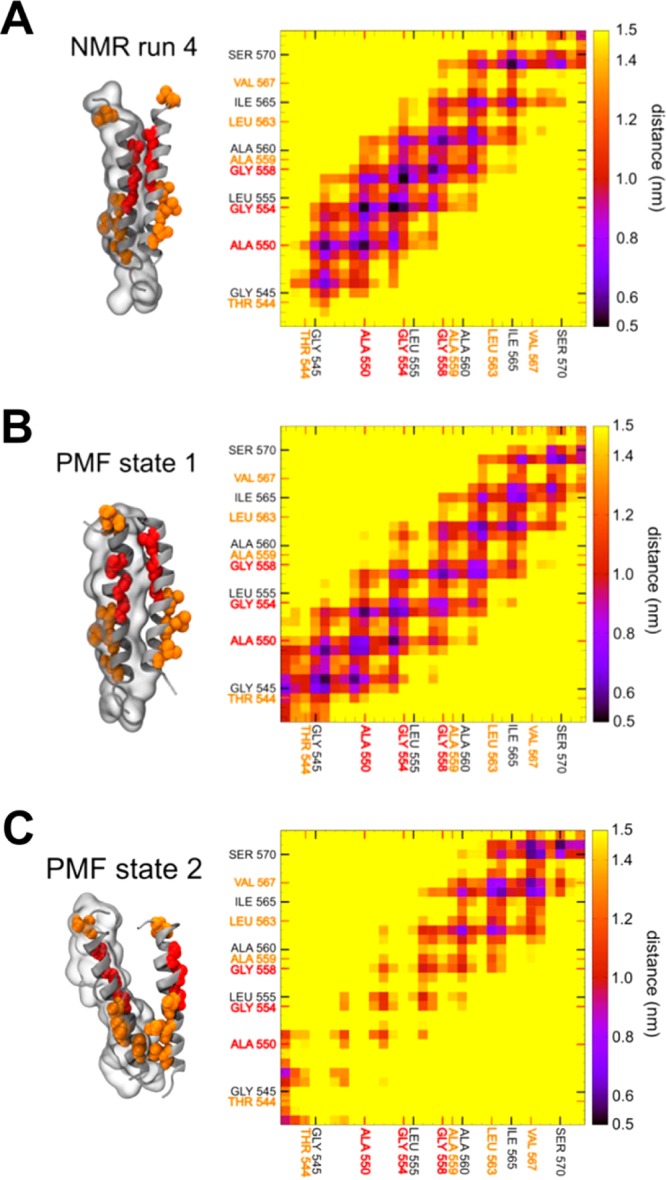
Atomistic simulations starting from two structures were selected from the NMR-based CG simulations and two structures from the unrestrained CG simulations based on PMF models (one structure representing State 1, and the other, State 2). In each case, a contact map and a representative structure of the helix dimer derived from the last 10 ns of the corresponding AT simulations are shown. For one helix, the surface is represented as a transparent envelope. Residues shown in red and orange are as previously described.
Significantly, the atomistic simulation based on State 2 revealed a (partial) TM helix dissociation event. During this event, disruption of the T544 interaction initiated a structural transition in which the glycine zipper distance increased to 1.7 nm. This disruption was driven by the creation of an intrahelix interaction between the carboxyl group of the side chain of E547 and backbone amide of T544 (see Supporting Information Figure S9 and Table S1). This interaction was also identified by Bocharov et al.12 At that point, only the C-terminal residues continued to interact (Figure 7C). Extending this simulation to 200 ns did not result in a complete dissociation of the helices, as a number of residues, e.g., R572, R571, S570, F568, or V567, continued to interact (data not shown).
Due to the short time scale of AT simulations (<100 ns), we have not explored beyond a small, local fraction of the energy landscape, so these AT simulations were more important to refine our CG models. Nevertheless, the atomistic simulations suggest that by starting from different structures yielded by the CG simulations one may explore the conformation and local dynamics of the EphA1 TM helix dimer, highlighting a stable right-handed (State 1) conformation, intermediate states, and a (incomplete) helix dissociation event starting from the (metastable) State 2 configuration.
Discussion
Mechanistic and Structural Implications
Our simulations have revealed two different states of the EphA1 TM helix dimer, as was recently also suggested by Li et al.64 In the current study, it was also possible to characterize potential paths from one state to the other. This allows for an improved understanding of the transition between the two states, emphasizing a potential asymmetric dimer, as also suggested recently for other RTKs (e.g., refs (19 and 65)) but not previously for EphA1 or its close homologues. This has possible mechanistic implications that are consistent with a number of experimental and computational studies.
The State 1 configuration of the EphA1 dimer is in agreement both with the NMR structure12 and with other theoretical studies.46,64,66 In particular, our model reveals a dimer with a principal interaction around the glycine zipper motif A550X3G554X3G558, as seen in the NMR structure. This interaction is extended to residues in N- and C-terminal parts, e.g., G546 and L561L562 or I565L566 (see Figures 4 and S5). We note that Bocharov et al. proposed that this dimer may adopt different conformations and may be quite flexible, as suggested by high chemical shift changes.12 Furthermore, other models for this dimer also imply configurations with a large range of crossing angles, e.g., ref (66). On average, the crossing angle for State 1 is around −20°, in comparison with a value of −35° in the NMR structure. From our unrestrained CG simulations, this difference in crossing angles does not seem to be due to changes in membrane thickness. It is conceivable that it may reflect differences between the bilayer and bicelle environments, especially, e.g., interactions of the termini with lipid headgroups and also the possible effects of membrane curvature, as was suggested by a recent computational study of an unrelated system,67 but further studies will be required to explore this more systematically.
In contrast, the State 2 configuration exhibits an interface spread along the whole helix (interacting via residues T544X2E547I548X2V551X3L555X3A559X3L563X2L566V567). Bocharov et al. postulated that the EphA1 dimer could adopt a second conformation,12 proposing a second interaction site for the EphA1 dimer structure at two different potential positions: around the GG4-like motif A560X3G564 or via a heptad like motif IV549X5LL556X5LL563. Our model is broadly in agreement with their second proposed motif. We note that this is also in partial agreement with a left-handed model of EphA1 presented in recent studies by Li et al.64 We have not observed long-lasting dimerization through the A560X3G564 motif, although this motif was seen in transient helix interactions (e.g., Figure 4B). It is useful to note that the presence of a sequence motif does not seem to be sufficient to predict and explain TM dimerization.25 Furthermore, a sequence alignment presented by Muhle-Goll et al. indicated that this latter motif in EphA1 does not seem to be conserved across different receptor tyrosine kinase families.68 We superimposed our model of State 2 obtained from AT MD simulations with recent left-handed dimer structures obtained by NMR for EphA2 and PDGFR (Figure 8). The Cα RMSD is 0.3 nm between our State 2 model and the EphA2 structure and 0.33 nm between our State 2 model and the PDGFR structure. Furthermore, this structural alignment confirms that those residues at the interface in the two experimental left-handed structures also interact in our State 2 model. The interface of this model also seems to be in partial agreement with recent MD simulations of the Neu TM dimer in a DPPC bilayer.69 The crossing angle obtained in our model for State 2 is distributed around 0° (between −5° and +3°). This value is smaller than that seen in NMR structures for a left-handed dimer (between +15° and +23°28). Although we cannot exclude the possibility that the CG force field may have an influence on the crossing angle values, models constructed with other methodologies present crossing angle values in the same range; for example, models presented by Volynsky et al. have crossing angle values around 5° (see Supplementary Table 1 in ref (19)), and Prakash et al. have angles distributed around 0° (Figure 4 ref (39)). More recently, Li et al. proposed left-handed models for the EphA1 dimer with crossing angle ranging from +5° to +11° (Figure 4 ref (64)). This suggests a convergence of computational approaches.
Figure 8.
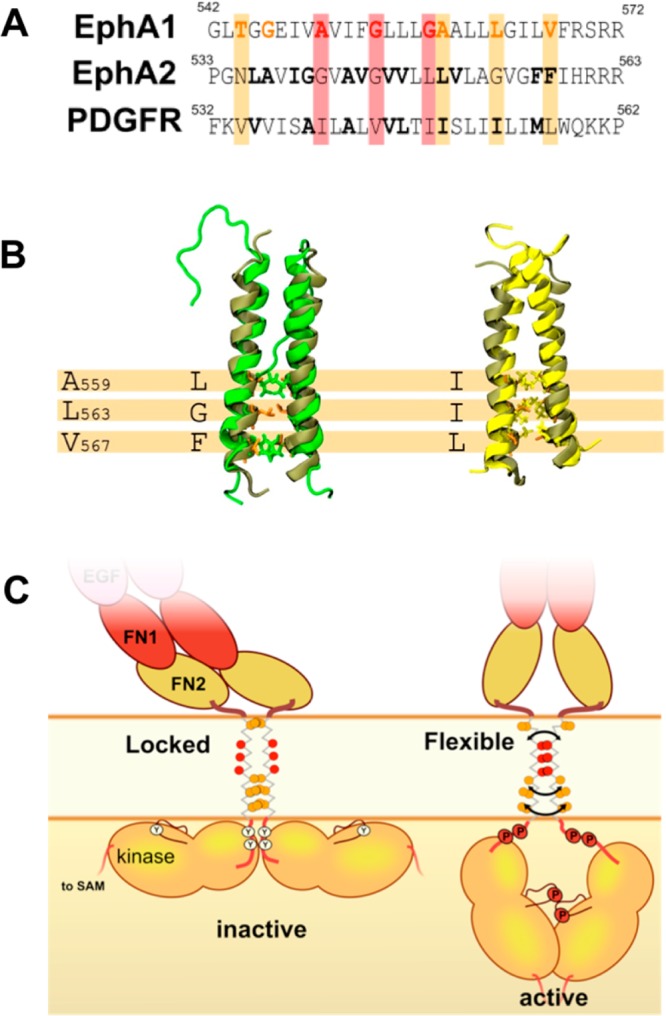
(A) Sequence alignment of the EphA1 TM helix with those of two recently determined TM dimer structures, namely, for EphA2 and PDGF. (B) Structural alignment of the EphA1 TM helix dimer (structure in tan; our model of State 2 was extracted from AT MD simulation starting with a State 2 structure having a crossing angle ca. +5°) with recently determined NMR structures for left-handed TM dimers of EphA2 (structure in green; PDB ID: 2K9Y) and of PDGFR (structure in yellow; PDB ID: 2L6W). (C) Schematic diagram depicting potential movements of the EphA1 receptor domains relative to the membrane. On the left, State 2 may lock the kinase domains in a configuration where some phosphorylation sites are not accessible and so the receptor is in an inactive state. On the right, due to the greater flexibility of State 1, the kinases sites are accessible and so may be phosphorylated, thus allowing the receptor to adopt an active state.
Overall, our results suggest a rotational mechanism for the transition from State 1 to State 2 (Figure 6 and Supporting Information Movies 1 and 2), with the TM helices rotating relative to one another along their respective axis. Such a rotational movement has been proposed for other related systems, e.g., refs (65 and 70). For example, Beevers et al. also noticed small rotation phenomenon during their 100 ns simulations of the Neu TM helix dimer,69 and Prakash et al. also postulated this type of rotation for the ErbB2 receptor TM domains.39 This rotational mechanism may sometimes also lead to an asymmetric dimer. Recently, Volynsky et al. highlighted asymmetric conformations for the FGFR3 dimer,19 and Reddy et al. also found an asymmetric dimer for FGFR3 mutants using MD simulations.65 Bocharov et al. also mentioned that the TM domain is involved in a micro- to millisecond conformational exchange12 and found that Glu547 can play an important role in the dimer interaction, interacting with Thr544 and thus presenting a substantive chemical shift difference as a function of pH.12 In our proposed pathway, the evolution from State 2 to State 1 involves the interactions of Thr544 and Glu547. These two residues can be involved in both inter- and intrahelical interactions (see Supporting Information Table S1), so it may be that the creation of intrahelical interactions weaken the interhelical interactions (Supporting Information Figures S9 and S10), facilitating the passage from State 2 to State 1, perhaps leading to a partial dissociation of the dimer, as seen for one AT simulation (Figure 7C). This implies a reorganization of the area around residues 547–550, in accordance with the variations of this area noticed by Bocharov et al.
These observations are consistent with a rotation-coupled activation mechanism for the EphA1 receptor.12 Although one must exercise caution in extrapolating from the behavior of a TM helix dimer to the whole EphA1 receptor, we suggest that the rotations of TM helices along their axes may result in a rotation of the kinase domains. State 2, through an interaction stabilized along the whole helix, may hold the kinases in a locked position, whereas the C-terminal part of the helices in State 1 seems to be more flexible and may provide greater freedom for rearrangements of the juxtamembrane and kinase domains (Figure 8C). In the case of State 2, the locked conformation may hold the kinase domain close to the membrane and so obscure phosphorylation and activation sites, as suggested by studies on EphA371 and EGFR,7 whereas State 1 would provide more flexibility to expose the different sites to be phosphorylated (Figure 8C). The substantial ectodomain is also flexible, so it is more difficult to infer an effect of the TM dimerization mode on it. Nevertheless, it has recently been postulated that a large rearrangement of the ectodomain occurs between the activated and inactivated states for the EphA2 receptor is linked to changes in packing of the TM domains.14 Using this model as a template for EphA1, we suggest that the State 2 conformation will lock the ectodomain in a preformed inactive state where the two ectodomains are staggered, as seen in a structure of unliganded EphA2 ectodomain dimer.10 State 1 will allow greater displacements of the FN2 domains near the membrane to adopt a wider spacing between the two FN2 domains, as seen for the ligand-bound form of the EphA2 dimer.10 Thus, State 1 may be related to an active state, whereas State 2 may be linked to an inactive state,14 as has also been suggested for FGFR319 and EGFR.18 A comparable mechanism was recently postulated by Bocharov et al. in their “string-puppet” model for the FGFR3 receptor.8 A question remains: does the free energy landscape of the dimer directly drive the adoption of active vs inactive states? Due to the size of the cytosolic and extracellular domains, we doubt that this is the case, but the dimer energetics may determine the passage from one state to the other. Thus, receptor activation may be the result of fine dynamic balance at each level, extracellular, membrane, and cytosolic, and it is the reinforcement or the antagonism of these different components that would drive a global movement. It will therefore be important to model the whole receptor to better understand these combinatorial and multifaceted dynamic balances.
Free Energies of Dimerization
Our PMF calculations, based on the glycine motif separation, reveal two states of the EphA1 TM helix dimer, and these are supported by unrestrained simulations. However, there are difficulties inherent in comparing absolute dimerization free energies both between simulations and experiments and between different simulations. In particular, experimental as well as theoretical analyses of TM dimerization may be quite sensitive to parameter changes, making quantitative comparisons difficult at present.
The free energy difference between the fully separated EphA1 TM helices (at a separation of >2.5 nm) and the dimerized State 1 is ca. −60 ± 2 kJ/mol. This is significantly larger than an experimental estimate of the association free energy of −15 kJ/mol, as measured using FRET in DMPC liposomes.16 It is important to remain aware that estimates of the association free energy of TM helices may be sensitive to both the exact extent of the TM helix construct66 and to the membrane (or membrane-like) environment employed.72,73 Furthermore, FRET is, to some extent, an indirect probe of dimerization free energy, corresponding to a finite local concentration, in contrast to the limit of infinite dilution when the helices are separated. Thus, it is informative to deconstruct the disagreement between experiment and simulation.
As a point of reference, one may consider the free energy of dimerization of the TM domain of glycophorin A (GpA). Experimentally, this can range from ca. −30 kJ/mol in, e.g., C8E5 detergent micelles74 to ca. −15 kJ/mol in plasma membrane-derived vesicles.75 Computationally, estimates include ca. −45 kJ/mol (from atomistic simulations in a membrane-mimetic dodecane slab)35 and ca. −3037 to −4036 kJ/mol via CG simulations in lipid bilayers. Thus, both experimental and computational estimates range quite widely.
CG simulations have been used to estimate PMFs for a number of TM helix dimers, with free energy differences between the fully separated TM helices and the dimerized state as follows: −3037 and −45 kJ/mol for GpA,36 −21 kJ/mol for ErbB1 to −33 kJ/mol for ErbB4 homodimers,38 and −58 kJ/mol for the neuropilin 1/plexin A1 TM helix heterodimer.76 Thus, our estimate for the EphA1 State 1 TM dimer is comparable to estimates for related systems using the MARTINI force field.
From a purely simulation-based perspective, sampling in our free energy calculations was checked by calculating the statistical inefficiency following Yang et al.54 This allows one to define the converged part of the simulation. Using this criterion, we considered the last 10% of the simulation as fully converged (see Supporting Information Text and Figure S1). Furthermore, the depth and shape of the PMF profiles generated are similar to those for GpA, calculated using an either atomistic model35 or the MARTINI CG model.36
Although our multiscale approach reveals key aspects of the dynamics and energetics of the EphA1 TM dimer, our understanding of this system remains incomplete. The PMF profile is based on a one-dimensional helix separation and so depends on the reaction coordinate chosen (here, the glycine motif separation distance). Other reaction coordinates such as crossing angle, helix tilt, etc. may have an influence on the energy profile. Therefore, in the future, we would like to extend these studies results to 2D PMF calculations,64 possibly combined with advanced sampling methods,77 in order to provide a fuller characterization of the free energy landscape of helix–helix interactions in this system. Another point on which to reflect is the stability of the State 2 model in our simulations. Even if our CG results compare reasonably well with other computational studies, many of these studies are based on the same force field. Indeed, during the short AT MD simulations starting from the State 2, we have seen the early stages of helix-dimer dissociation. It would be interesting to perform longer time scale simulations on TM dimers using different force fields (in a study comparable to recent work on small water-soluble proteins62) to enable a more critical comparison of TM helix modeling at different granularities.
Wider Implications
Overall, this study suggests that the interaction of TM helices in EphA1 RTK dimers is intrinsically dynamic, reflecting a complex energy landscape for interaction with multiple local minima. Our study provides a novel interpretation of previous experimental results,12,66 showing two states for EphA1 dimerization. We suggest that there is a rotational pathway to pass from one state to the other. These observations are consistent with a rotation-coupled activation mechanism that has been postulated to govern the EphA1 system. This provides a potential mechanism for signaling whereby both extracellular and intracellular events can be linked to a repopulation of the underlying TM helix dimer landscape rather than a simple process of switching between two states. Related models have been suggested for EphA2,14 FGFR3,19 and EGFR.7,18 This suggests a degree of convergence on a model in which the TM dimers of RTK tranmembrane dimers readily exchange between conformations. Thus, these studies stress the need to fully understand the dynamic behavior of the TM dimers of RTKs from a mechanistic perspective and also to exploit our understanding for the design of, e.g., peptides that target receptor TM domains.78
Supporting Information Available
Additional analysis of the simulations and movies of the State 2 to State 1 transition. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Supplementary Material
References
- Kullander K.; Klein R. (2002) Mechanisms and functions of Eph and ephrin signalling. Nat. Rev. Mol. Cell Biol. 3, 475–486. [DOI] [PubMed] [Google Scholar]
- Qin H.; Noberini R.; Huan X.; Shi J.; Pasquale E.; Song J. (2010) Structural characterization of the EphA4–Ephrin-B2 complex reveals new features enabling Eph–ephrin binding promiscuity. J. Biol. Chem. 285, 644–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowden T. A.; Aricescu A. R.; Nettleship J. E.; Siebold C.; Rahman-Huq N.; Owens R. J.; Stuart D. I.; Jones E. Y. (2009) Structural plasticity of Eph receptor A4 facilitates cross-class ephrin signaling. Structure 17, 1386–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolov D. B.; Xu K.; Himanen J. P. (2013) Eph/ephrin recognition and the role of Eph/ephrin clusters in signaling initiation. Biochim. Biophys. Acta 1834, 2160–2165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama I. N. (2014) Mechanisms of activation of receptor tyrosine kinases: monomers or dimers. Cells 3, 304–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlessinger J. (2014) Receptor tyrosine kinases: legacy of the first two decades. Cold Spring Harbor Perspect. Biol. 6, a008912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkhipov A.; Shan Y.; Das R.; Endres N. F.; Eastwood M. P.; Wemmer D. E.; Kuriyan J.; Shaw D. E. (2013) Architecture and membrane interactions of the EGF receptor. Cell 152, 557–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocharov E. V.; Lesovoy D. M.; Goncharuk S. A.; Goncharuk M. V.; Hristova K.; Arseniev A. S. (2013) Structure of FGFR3 transmembrane domain dimer: implications for signaling and human pathologies. Structure 21, 2087–2093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He L. J.; Hristova K. (2012) Physical–chemical principles underlying RTK activation, and their implications for human disease. Biochim. Biophys. Acta 1818, 995–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seiradake E.; Harlos K.; Sutton G.; Aricescu A.; Jones E. (2010) An extracellular steric seeding mechanism for Eph–ephrin signaling platform assembly. Nat. Struct. Mol. Biol. 17, 398–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himanen J. P.; Yermekbayeva L.; Janes P. W.; Walker J. R.; Xu K.; Atapattu L.; Rajashankar K. R.; Mensinga A.; Lackmann M.; Nikolov D. B.; Dhe-Paganon S. (2010) Architecture of Eph receptor clusters. Proc. Natl. Acad. Sci. U.S.A. 107, 10860–10865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocharov E. V.; Mayzel M. L.; Volynsky P. E.; Goncharuk M. V.; Ermolyuk Y. S.; Schulga A. A.; Artemenko E. O.; Efremov R. G.; Arseniev A. S. (2008) Spatial structure and pH-dependent conformational diversity of dimeric transmembrane domain of the receptor tyrosine kinase EphA1. J. Biol. Chem. 283, 29385–29395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocharov E. V.; Mayzel M. L.; Volynsky P. E.; Mineev K. S.; Tkach E. N.; Ermolyuk Y. S.; Schulga A. A.; Efremov R. G.; Arseniev A. S. (2010) Left-handed dimer of EphA2 transmembrane domain: helix packing diversity among receptor tyrosine kinases. Biophys. J. 98, 881–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharonov G.; Bocharov E.; Kolosov P.; Astapova M.; Arseniev A.; Feofanov A. (2014) Point mutations in dimerization motifs of transmembrane domain stabilize active or inactive state of the EphA2 receptor tyrosine kinase. J. Biol. Chem. 289, 14955–14964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himanen J.; Yermekbayeva L.; Janes P.; Walker J.; Xu K.; Atapattu L.; Rajashankar K.; Mensinga A.; Lackmann M.; Nikolov D.; Dhe-Paganon S. (2010) Architecture of Eph receptor clusters. Proc. Natl. Acad. Sci. U.S.A. 107, 10860–10865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artemenko E.; Egorova N.; Arseniev A.; Feofanov A. (2008) Transmembrane domain of EphA1 receptor forms dimers in membrane-like environment. Biochim. Biophys. Acta 1778, 2361–2367. [DOI] [PubMed] [Google Scholar]
- Hubert P.; Sawma P.; Duneau J.-P.; Khao J.; Hénin J.; Bagnard D.; Sturgis J. (2010) Single-spanning transmembrane domains in cell growth and cell-cell interactions: more than meets the eye?. Cell Adhes. Migr. 4, 313–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endres N. F.; Das R.; Smith A. W.; Arkhipov A.; Kovacs E.; Huang Y. J.; Pelton J. G.; Shan Y. B.; Shaw D. E.; Wemmer D. E.; Groves J. T.; Kuriyan J. (2013) Conformational coupling across the plasma membrane in activation of the EGF receptor. Cell 152, 543–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volynsky P. E.; Polyansky A. A.; Fakhrutdinova G. N.; Bocharov E.; Efremov R. G. (2013) Role of dimerization efficiency of transmembrane domains in activation of fibroblast growth factor receptor 3. J. Am. Chem. Soc. 135, 8105–8108. [DOI] [PubMed] [Google Scholar]
- Sarabipour S.; Hristova K. (2013) FGFR3 transmembrane domain interactions persist in the presence of its extracellular domain. Biophys. J. 105, 165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks A. J.; Dai W.; O’Mara M. L.; Abankwa D.; Chhabra Y.; Pelekanos R. A.; Gardon O.; Tunny K. A.; Blucher K. M.; Morton C. J.; Parker M. W.; Sierecki E.; Gambin Y.; Gomez G. A.; Alexandrov K.; Wilson I. A.; Doxastakis M.; Mark A. E.; Waters M. J. (2014) Mechanism of activation of protein kinase JAK2 by the growth hormone receptor. Science 344, 1249783 . [DOI] [PubMed] [Google Scholar]
- Lee J.; Miyazaki M.; Romeo G. R.; Shoelson S. E. (2014) Insulin receptor activation with transmembrane domain ligands. J. Biol. Chem. 289, 19769–19777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langosch D.; Arkin I. T. (2009) Interaction and conformational dynamics of membrane-spanning protein helices. Protein Sci. 18, 1343–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews E.; Zoonens M.; Engelman D. (2006) Dynamic helix interactions in transmembrane signaling. Cell 127, 447–450. [DOI] [PubMed] [Google Scholar]
- Li E.; Wimley W.; Hristova K. (2012) Transmembrane helix dimerization: beyond the search for sequence motifs. Biochim. Biophys. Acta 1818, 183–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternberg M. J. E.; Gullick W. J. (1990) A sequence motif in the transmembrane region of growth factor receptors with tyrosine kinase activity mediates dimerization. Prot. Eng. 3, 245–248. [DOI] [PubMed] [Google Scholar]
- MacKenzie K. R.; Prestegard J. H.; Engelman D. M. (1997) A transmembrane helix dimer: structure and implications. Science 276, 131–133. [DOI] [PubMed] [Google Scholar]
- Cymer F.; Veerappan A.; Schneider D. (2012) Transmembrane helix-helix interactions are modulated by the sequence context and by lipid bilayer properties. Biochim. Biophys. Acta 1818, 963–973. [DOI] [PubMed] [Google Scholar]
- Finger C.; Escher C.; Schneider D. (2009) The single transmembrane domain of human tyrosine kinases encode self interactions. Science Signal. 2, 51–58. [DOI] [PubMed] [Google Scholar]
- Fink A.; Sal-Man N.; Gerber D.; Shai Y. (2012) Transmembrane domains interactions within the membrane milieu: principles, advances and challenges. Biochim. Biophys. Acta 1818, 974–983. [DOI] [PubMed] [Google Scholar]
- Russ W. P.; Engelman D. M. (1999) TOXCAT: a measure of transmembrane helix association in a biological membrane. Proc. Natl. Acad. Sci. U.S.A. 96, 863–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You M.; Li E.; Wimley W.; Hristova K. (2005) Forster resonance energy transfer in liposomes: measurements of transmembrane helix dimerization in the native bilayer environment. Anal. Biochem. 340, 154–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming K. G.; Ackerman A. L.; Engelman D. M. (1997) The effect of point mutations on the free energy of transmembrane alpha-helix dimerization. J. Mol. Biol. 272, 266–275. [DOI] [PubMed] [Google Scholar]
- Fleming K. G.; Engelman D. M. (2001) Specificity in transmembrane helix–helix interactions can define a hierarchy of stability for sequence variants. Proc. Natl. Acad. Sci. U.S.A. 98, 14340–14344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hénin J.; Pohorille A.; Chipot C. (2005) Insights into the recognition and association of transmembrane α-helices. The free energy of α-helix dimerization in glycophorin A. J. Am. Chem. Soc. 127, 8478–8484. [DOI] [PubMed] [Google Scholar]
- Sengupta D.; Marrink S. J. (2010) Lipid-mediated interactions tune the association of glycophorin A helix and its disruptive mutants in membranes. Phys. Chem. Chem. Phys. 12, 12987–12996. [DOI] [PubMed] [Google Scholar]
- Janosi L.; Prakash A.; Doxastakis M. (2010) Lipid-modulated sequence-specific association of glycophorin A in membranes. Biophys. J. 99, 284–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash A.; Janosi L.; Doxastakis M. (2010) Self-association of models of transmembrane domains of ErbB receptors in a lipid bilayer. Biophys. J. 99, 3657–3665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prakash A.; Janosi L.; Doxastakis M. (2011) GxxxG motifs, phenylalanine, and cholesterol guide the self-association of transmembrane domains of ErbB2 receptors. Biophys. J. 101, 1949–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polyansky A. A.; Volynsky P. E.; Efremov R. G. (2012) Multistate organization of transmembrane helical protein dimers governed by the host membrane. J. Am. Chem. Soc. 134, 14390–14400. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada J.; Yefimov S.; Tieleman D. P.; de Vries A. H. (2007) The MARTINI forcefield: coarse grained model for biomolecular simulations. J. Phys. Chem. B 111, 7812–7824. [DOI] [PubMed] [Google Scholar]
- Monticelli L.; Kandasamy S. K.; Periole X.; Larson R. G.; Tieleman D. P.; Marrink S. J. (2008) The MARTINI coarse grained force field: extension to proteins. J. Chem. Theory Comput. 4, 819–834. [DOI] [PubMed] [Google Scholar]
- Kalli A. C.; Hall B. A.; Campbell I. D.; Sansom M. S. P. (2011) A helix heterodimer in a lipid bilayer: structure prediction of the structure of an integrin transmembrane domain via multiscale simulations. Structure 19, 1477–1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Psachoulia E.; Bond P. J.; Fowler P. W.; Sansom M. S. P. (2008) Helix–helix interactions in membrane proteins: coarse grained simulations of glycophorin helix dimerization. Biochem. 47, 10503–105012. [DOI] [PubMed] [Google Scholar]
- Wei P.; Zheng B.-K.; Guo P.-R.; Kawakami T.; Luo S.-Z. (2013) The association of polar residues in the DAP12 homodimer: TOXCAT and molecular dynamics simulation studies. Biophys. J. 104, 1435–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L. Q.; Sodt A. J.; Venable R. M.; Pastor R. W.; Buck M. (2013) Prediction, refinement, and persistency of transmembrane helix dimers in lipid bilayers using implicit and explicit solvent/lipid representations: microsecond molecular dynamics simulations of ErbB1/B2 and EphA1. Proteins: Struct., Funct., Bioinf. 81, 365–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volynsky P. E.; Mineeva E. A.; Goncharuk M. V.; Ermolyuk Y. S.; Arseniev A. S.; Efremov R. G. (2010) Computer simulations and modeling-assisted ToxR screening in deciphering 3D structures of transmembrane α-helical dimers: ephrin receptor A1. Phys. Biol. 7, 15. [DOI] [PubMed] [Google Scholar]
- Bond P. J.; Sansom M. S. P. (2006) Insertion and assembly of membrane proteins via simulation. J. Am. Chem. Soc. 128, 2697–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond P. J.; Wee C. L.; Sansom M. S. P. (2008) Coarse-grained molecular dynamics simulations of the energetics of helix insertion into a lipid bilayer. Biochemistry 47, 11321–11331. [DOI] [PubMed] [Google Scholar]
- Bond P. J.; Faraldo-Gómez J. D.; Deol S. S.; Sansom M. S. P. (2006) Membrane protein dynamics and detergent interactions within a crystal: a simulation study of OmpA. Proc. Natl. Acad. Sci. U.S.A. 103, 9518–9523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond P. J.; Holyoake J.; Ivetac A.; Khalid S.; Sansom M. S. P. (2007) Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J. Struct. Biol. 157, 593–605. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. (2008) GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4, 435–447. [DOI] [PubMed] [Google Scholar]
- Roux B. (1995) The calculation of the potential of mean force using computer simulations. Comput. Phys. Commun. 91, 275–282. [Google Scholar]
- Yang W.; Bitetti-Putzer R.; Karplus M. (2004) Free energy simulations: use of reverse cumulative averaging to determine the equilibrated region and the time required for convergence. J. Chem. Phys. 120, 2618–2628. [DOI] [PubMed] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R.; Kollman P. (1992) The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 13, 1011–1021. [Google Scholar]
- Stansfeld P. J.; Sansom M. S. P. (2011) From coarse-grained to atomistic: a serial multi-scale approach to membrane protein simulations. J. Chem. Theory Comput. 7, 1157–1166. [DOI] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. (1993) Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092. [Google Scholar]
- Parrinello M.; Rahman A. (1981) Polymorphic transitions in single-crystals: a new molecular-dynamics method. J. Appl. Phys. 52, 7182–7190. [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. (2007) Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101. [DOI] [PubMed] [Google Scholar]
- Hall B. A.; Halim K. A.; Buyan A.; Emmanouil B.; Sansom M. S. P. (2014) Sidekick for membrane simulations: automated ensemble molecular dynamics simulations of transmembrane helices. J. Chem. Theory Comput. 10, 2165–2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. (1996) VMD - Visual Molecular Dynamics. J. Mol. Graph. 14, 33–38. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Maragakis P.; Piana S.; Eastwood M. P.; Dror R. O.; Shaw D. E. (2012) Systematic validation of protein force fields against experimental data. PLoS One 7, e32131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale C.; Bennett W.; Tieleman D.; R P. (2011) Statistical convergence of equilibrium properties in simulations of molecular solutes embedded in lipid bilayers. J. Chem. Theory Comput. 7, 4175–4188. [DOI] [PubMed] [Google Scholar]
- Li P. C.; Miyashita N.; Im W.; Ishido S.; Sugita Y. (2013) Multidimensional umbrella sampling and replica–exchange molecular dynamics simulations for structure prediction of transmembrane helix dimers. J. Comput. Chem. 35, 300–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy T.; Manrique S.; Buyan A.; Hall B. A.; Chetwynd A.; Sansom M. S. P. (2014) Primary and secondary dimer interfaces of the FGFR3 transmembrane domain: characterization via multiscale molecular dynamics simulations. Biochemistry 53, 323–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volynsky P.; Mineeva E.; Goncharuk M.; Ermolyuk Y.; Arseniev A.; Efremov R. (2010) Computer simulations and modeling-assisted ToxR screening in deciphering 3D structures of transmembrane α-helical dimers: ephrin receptor A1. Phys. Biol. 7, 16014. [DOI] [PubMed] [Google Scholar]
- Dominguez L.; Meredith S. C.; Straub J. E.; Thirumalai D. (2014) Transmembrane fragment structures of amyloid precursor protein depend on membrane surface curvature. J. Am. Chem. Soc. 136, 854–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muhle-Goll C.; Hoffmann S.; Afonin S.; Grage S.; Polyansky A.; Windisch D.; Zeitler M.; Bürck J.; Ulrich A. (2012) Hydrophobic matching controls the tilt and stability of the dimeric platelet-derived growth factor receptor (PDGFR) β transmembrane segment. J. Biol. Chem. 287, 26178–26186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beevers A.; Nash A.; Salazar-Cancino M.; Scott D.; Notman R.; Dixon A. (2012) Effects of the oncogenic V664E mutation on membrane insertion, structure, and sequence-dependent interactions of the Neu transmembrane domain in micelles and model membranes: an integrated biophysical and simulation study. Biochemistry 51, 2558–2668. [DOI] [PubMed] [Google Scholar]
- Fleishman S. J.; Schlessinger J.; Ben-Tal N. (2002) A putative molecular-activation switch in the transmembrane domain of erbB2. Proc. Natl. Acad. Sci. U.S.A. 99, 15937–15940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes P. W.; Wimmer-Kleikamp S. H.; Frangakis A. S.; Treble K.; Griesshaber B.; Sabet O.; Grabenbauer M.; Ting A. Y.; Saftig P.; Bastiaens P. I.; Lackmann M. (2009) Cytoplasmic relaxation of active Eph controls Ephrin shedding by ADAM10. PLoS Biol. 7, e1000215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher L.; Engelman D.; Sturgis J. (2003) Effect of detergents on the association of the glycophorin a transmembrane helix. Biophys. J. 85, 3097–3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J.; Lazaridis T. (2006) Calculating the free energy of association of transmembrane helices. Biophys. J. 91, 1710–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming K. G. (2002) Standardizing the free energy change of transmembrane helix-helix interactions. J. Mol. Biol. 323, 563–571. [DOI] [PubMed] [Google Scholar]
- Sarabipour S.; Hristova K. (2013) Glycophorin A transmembrane domain dimerization in plasma membrane vesicles derived from CHO, HEK 293T, and A431 cells. Biochim. Biophys. Acta 1828, 1829–1833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aci-Sèche S.; Sawma P.; Hubert P.; Sturgis J. N.; Bagnard D.; Jacob L.; Genest M.; Garnier N. (2014) Transmembrane recognition of the semaphorin co-receptors neuropilin 1 and plexin A1: coarse-grained simulations. PLoS One 9, e97779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barducci A.; Bonomi M.; Prakash M.; Parrinello M. (2013) Free-energy landscape of protein oligomerization from atomistic simulations. Proc. Natl. Acad. Sci. U.S.A. 110, E4708–E4713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin H.; Slusky J. S.; Berger B. W.; Walters R. S.; Vilaire G.; Litvinov R. I.; Lear J. D.; Caputo G. A.; Bennett J. S.; DeGrado W. F. (2007) Computational design of peptides that target transmembrane helices. Science 315, 1817–1822. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


